forked from idrl/idrlnet
docs: Init commit
This commit is contained in:
parent
b470be21ca
commit
506c852c5e
|
|
@ -0,0 +1,129 @@
|
|||
# Byte-compiled / optimized / DLL files
|
||||
__pycache__/
|
||||
*.py[cod]
|
||||
*$py.class
|
||||
|
||||
# C extensions
|
||||
*.so
|
||||
|
||||
# Distribution / packaging
|
||||
.Python
|
||||
build/
|
||||
develop-eggs/
|
||||
dist/
|
||||
downloads/
|
||||
eggs/
|
||||
.eggs/
|
||||
lib/
|
||||
lib64/
|
||||
parts/
|
||||
sdist/
|
||||
var/
|
||||
wheels/
|
||||
*.egg-info/
|
||||
.installed.cfg
|
||||
*.egg
|
||||
MANIFEST
|
||||
|
||||
# PyInstaller
|
||||
# Usually these files are written by a python script from a template
|
||||
# before PyInstaller builds the exe, so as to inject date/other infos into it.
|
||||
*.manifest
|
||||
*.spec
|
||||
|
||||
# Installer logs
|
||||
pip-log.txt
|
||||
pip-delete-this-directory.txt
|
||||
|
||||
# Unit test / coverage reports
|
||||
htmlcov/
|
||||
.tox/
|
||||
.coverage
|
||||
.coverage.*
|
||||
.cache
|
||||
nosetests.xml
|
||||
coverage.xml
|
||||
*.cover
|
||||
.hypothesis/
|
||||
.pytest_cache/
|
||||
|
||||
# Translations
|
||||
*.mo
|
||||
*.pot
|
||||
|
||||
# Django stuff:
|
||||
*.log
|
||||
local_settings.py
|
||||
db.sqlite3
|
||||
|
||||
# Flask stuff:
|
||||
instance/
|
||||
.webassets-cache
|
||||
|
||||
# Scrapy stuff:
|
||||
.scrapy
|
||||
|
||||
# Sphinx documentation
|
||||
docs/_build/
|
||||
|
||||
# Dash docset
|
||||
docs/dash/
|
||||
|
||||
# PyBuilder
|
||||
target/
|
||||
|
||||
# Jupyter Notebook
|
||||
.ipynb_checkpoints
|
||||
|
||||
# pyenv
|
||||
.python-version
|
||||
|
||||
# celery beat schedule file
|
||||
celerybeat-schedule
|
||||
|
||||
# SageMath parsed files
|
||||
*.sage.py
|
||||
|
||||
# Environments
|
||||
.env
|
||||
.venv
|
||||
env/
|
||||
venv/
|
||||
ENV/
|
||||
env.bak/
|
||||
venv.bak/
|
||||
include/
|
||||
|
||||
# Spyder project settings
|
||||
.spyderproject
|
||||
.spyproject
|
||||
|
||||
# Rope project settings
|
||||
.ropeproject
|
||||
|
||||
# mkdocs documentation
|
||||
/site
|
||||
|
||||
# mypy
|
||||
.mypy_cache/
|
||||
|
||||
# notebooks
|
||||
notebooks/
|
||||
|
||||
# PyCharm related
|
||||
.idea/
|
||||
|
||||
# VSCode
|
||||
.vscode/
|
||||
/share/
|
||||
/etc/
|
||||
/bin/
|
||||
|
||||
# cache
|
||||
*.vtu
|
||||
*.csv
|
||||
*.npz
|
||||
*.ckpt
|
||||
events.out*
|
||||
*.png
|
||||
*.mat
|
||||
|
|
@ -0,0 +1,27 @@
|
|||
FROM pytorch/pytorch:1.7.0-cuda11.0-cudnn8-devel
|
||||
RUN apt-get update && apt-get install -y openssh-server nfs-common && \
|
||||
echo "PermitRootLogin yes" >> /etc/ssh/sshd_config && \
|
||||
(echo '123456'; echo '123456') | passwd root
|
||||
|
||||
RUN pip install -i https://pypi.mirrors.ustc.edu.cn/simple/ transforms3d \
|
||||
typing \
|
||||
numpy \
|
||||
keras \
|
||||
h5py \
|
||||
pandas \
|
||||
zipfile36 \
|
||||
scikit-optimize \
|
||||
pytest \
|
||||
sphinx \
|
||||
matplotlib \
|
||||
myst_parser \
|
||||
sphinx_rtd_theme==0.5.2 \
|
||||
tensorboard==2.4.1 \
|
||||
sympy==1.5.1 \
|
||||
pyevtk==1.1.1 \
|
||||
flask==1.1.2 \
|
||||
requests==2.25.0 \
|
||||
networkx==2.5.1
|
||||
COPY . /idrlnet/
|
||||
RUN cd /idrlnet && pip install -e .
|
||||
ENTRYPOINT service ssh start && bash
|
||||
|
|
@ -0,0 +1,202 @@
|
|||
|
||||
Apache License
|
||||
Version 2.0, January 2004
|
||||
http://www.apache.org/licenses/
|
||||
|
||||
TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION
|
||||
|
||||
1. Definitions.
|
||||
|
||||
"License" shall mean the terms and conditions for use, reproduction,
|
||||
and distribution as defined by Sections 1 through 9 of this document.
|
||||
|
||||
"Licensor" shall mean the copyright owner or entity authorized by
|
||||
the copyright owner that is granting the License.
|
||||
|
||||
"Legal Entity" shall mean the union of the acting entity and all
|
||||
other entities that control, are controlled by, or are under common
|
||||
control with that entity. For the purposes of this definition,
|
||||
"control" means (i) the power, direct or indirect, to cause the
|
||||
direction or management of such entity, whether by contract or
|
||||
otherwise, or (ii) ownership of fifty percent (50%) or more of the
|
||||
outstanding shares, or (iii) beneficial ownership of such entity.
|
||||
|
||||
"You" (or "Your") shall mean an individual or Legal Entity
|
||||
exercising permissions granted by this License.
|
||||
|
||||
"Source" form shall mean the preferred form for making modifications,
|
||||
including but not limited to software source code, documentation
|
||||
source, and configuration files.
|
||||
|
||||
"Object" form shall mean any form resulting from mechanical
|
||||
transformation or translation of a Source form, including but
|
||||
not limited to compiled object code, generated documentation,
|
||||
and conversions to other media types.
|
||||
|
||||
"Work" shall mean the work of authorship, whether in Source or
|
||||
Object form, made available under the License, as indicated by a
|
||||
copyright notice that is included in or attached to the work
|
||||
(an example is provided in the Appendix below).
|
||||
|
||||
"Derivative Works" shall mean any work, whether in Source or Object
|
||||
form, that is based on (or derived from) the Work and for which the
|
||||
editorial revisions, annotations, elaborations, or other modifications
|
||||
represent, as a whole, an original work of authorship. For the purposes
|
||||
of this License, Derivative Works shall not include works that remain
|
||||
separable from, or merely link (or bind by name) to the interfaces of,
|
||||
the Work and Derivative Works thereof.
|
||||
|
||||
"Contribution" shall mean any work of authorship, including
|
||||
the original version of the Work and any modifications or additions
|
||||
to that Work or Derivative Works thereof, that is intentionally
|
||||
submitted to Licensor for inclusion in the Work by the copyright owner
|
||||
or by an individual or Legal Entity authorized to submit on behalf of
|
||||
the copyright owner. For the purposes of this definition, "submitted"
|
||||
means any form of electronic, verbal, or written communication sent
|
||||
to the Licensor or its representatives, including but not limited to
|
||||
communication on electronic mailing lists, source code control systems,
|
||||
and issue tracking systems that are managed by, or on behalf of, the
|
||||
Licensor for the purpose of discussing and improving the Work, but
|
||||
excluding communication that is conspicuously marked or otherwise
|
||||
designated in writing by the copyright owner as "Not a Contribution."
|
||||
|
||||
"Contributor" shall mean Licensor and any individual or Legal Entity
|
||||
on behalf of whom a Contribution has been received by Licensor and
|
||||
subsequently incorporated within the Work.
|
||||
|
||||
2. Grant of Copyright License. Subject to the terms and conditions of
|
||||
this License, each Contributor hereby grants to You a perpetual,
|
||||
worldwide, non-exclusive, no-charge, royalty-free, irrevocable
|
||||
copyright license to reproduce, prepare Derivative Works of,
|
||||
publicly display, publicly perform, sublicense, and distribute the
|
||||
Work and such Derivative Works in Source or Object form.
|
||||
|
||||
3. Grant of Patent License. Subject to the terms and conditions of
|
||||
this License, each Contributor hereby grants to You a perpetual,
|
||||
worldwide, non-exclusive, no-charge, royalty-free, irrevocable
|
||||
(except as stated in this section) patent license to make, have made,
|
||||
use, offer to sell, sell, import, and otherwise transfer the Work,
|
||||
where such license applies only to those patent claims licensable
|
||||
by such Contributor that are necessarily infringed by their
|
||||
Contribution(s) alone or by combination of their Contribution(s)
|
||||
with the Work to which such Contribution(s) was submitted. If You
|
||||
institute patent litigation against any entity (including a
|
||||
cross-claim or counterclaim in a lawsuit) alleging that the Work
|
||||
or a Contribution incorporated within the Work constitutes direct
|
||||
or contributory patent infringement, then any patent licenses
|
||||
granted to You under this License for that Work shall terminate
|
||||
as of the date such litigation is filed.
|
||||
|
||||
4. Redistribution. You may reproduce and distribute copies of the
|
||||
Work or Derivative Works thereof in any medium, with or without
|
||||
modifications, and in Source or Object form, provided that You
|
||||
meet the following conditions:
|
||||
|
||||
(a) You must give any other recipients of the Work or
|
||||
Derivative Works a copy of this License; and
|
||||
|
||||
(b) You must cause any modified files to carry prominent notices
|
||||
stating that You changed the files; and
|
||||
|
||||
(c) You must retain, in the Source form of any Derivative Works
|
||||
that You distribute, all copyright, patent, trademark, and
|
||||
attribution notices from the Source form of the Work,
|
||||
excluding those notices that do not pertain to any part of
|
||||
the Derivative Works; and
|
||||
|
||||
(d) If the Work includes a "NOTICE" text file as part of its
|
||||
distribution, then any Derivative Works that You distribute must
|
||||
include a readable copy of the attribution notices contained
|
||||
within such NOTICE file, excluding those notices that do not
|
||||
pertain to any part of the Derivative Works, in at least one
|
||||
of the following places: within a NOTICE text file distributed
|
||||
as part of the Derivative Works; within the Source form or
|
||||
documentation, if provided along with the Derivative Works; or,
|
||||
within a display generated by the Derivative Works, if and
|
||||
wherever such third-party notices normally appear. The contents
|
||||
of the NOTICE file are for informational purposes only and
|
||||
do not modify the License. You may add Your own attribution
|
||||
notices within Derivative Works that You distribute, alongside
|
||||
or as an addendum to the NOTICE text from the Work, provided
|
||||
that such additional attribution notices cannot be construed
|
||||
as modifying the License.
|
||||
|
||||
You may add Your own copyright statement to Your modifications and
|
||||
may provide additional or different license terms and conditions
|
||||
for use, reproduction, or distribution of Your modifications, or
|
||||
for any such Derivative Works as a whole, provided Your use,
|
||||
reproduction, and distribution of the Work otherwise complies with
|
||||
the conditions stated in this License.
|
||||
|
||||
5. Submission of Contributions. Unless You explicitly state otherwise,
|
||||
any Contribution intentionally submitted for inclusion in the Work
|
||||
by You to the Licensor shall be under the terms and conditions of
|
||||
this License, without any additional terms or conditions.
|
||||
Notwithstanding the above, nothing herein shall supersede or modify
|
||||
the terms of any separate license agreement you may have executed
|
||||
with Licensor regarding such Contributions.
|
||||
|
||||
6. Trademarks. This License does not grant permission to use the trade
|
||||
names, trademarks, service marks, or product names of the Licensor,
|
||||
except as required for reasonable and customary use in describing the
|
||||
origin of the Work and reproducing the content of the NOTICE file.
|
||||
|
||||
7. Disclaimer of Warranty. Unless required by applicable law or
|
||||
agreed to in writing, Licensor provides the Work (and each
|
||||
Contributor provides its Contributions) on an "AS IS" BASIS,
|
||||
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or
|
||||
implied, including, without limitation, any warranties or conditions
|
||||
of TITLE, NON-INFRINGEMENT, MERCHANTABILITY, or FITNESS FOR A
|
||||
PARTICULAR PURPOSE. You are solely responsible for determining the
|
||||
appropriateness of using or redistributing the Work and assume any
|
||||
risks associated with Your exercise of permissions under this License.
|
||||
|
||||
8. Limitation of Liability. In no event and under no legal theory,
|
||||
whether in tort (including negligence), contract, or otherwise,
|
||||
unless required by applicable law (such as deliberate and grossly
|
||||
negligent acts) or agreed to in writing, shall any Contributor be
|
||||
liable to You for damages, including any direct, indirect, special,
|
||||
incidental, or consequential damages of any character arising as a
|
||||
result of this License or out of the use or inability to use the
|
||||
Work (including but not limited to damages for loss of goodwill,
|
||||
work stoppage, computer failure or malfunction, or any and all
|
||||
other commercial damages or losses), even if such Contributor
|
||||
has been advised of the possibility of such damages.
|
||||
|
||||
9. Accepting Warranty or Additional Liability. While redistributing
|
||||
the Work or Derivative Works thereof, You may choose to offer,
|
||||
and charge a fee for, acceptance of support, warranty, indemnity,
|
||||
or other liability obligations and/or rights consistent with this
|
||||
License. However, in accepting such obligations, You may act only
|
||||
on Your own behalf and on Your sole responsibility, not on behalf
|
||||
of any other Contributor, and only if You agree to indemnify,
|
||||
defend, and hold each Contributor harmless for any liability
|
||||
incurred by, or claims asserted against, such Contributor by reason
|
||||
of your accepting any such warranty or additional liability.
|
||||
|
||||
END OF TERMS AND CONDITIONS
|
||||
|
||||
APPENDIX: How to apply the Apache License to your work.
|
||||
|
||||
To apply the Apache License to your work, attach the following
|
||||
boilerplate notice, with the fields enclosed by brackets "[]"
|
||||
replaced with your own identifying information. (Don't include
|
||||
the brackets!) The text should be enclosed in the appropriate
|
||||
comment syntax for the file format. We also recommend that a
|
||||
file or class name and description of purpose be included on the
|
||||
same "printed page" as the copyright notice for easier
|
||||
identification within third-party archives.
|
||||
|
||||
Copyright 2021 idrl.site
|
||||
|
||||
Licensed under the Apache License, Version 2.0 (the "License");
|
||||
you may not use this file except in compliance with the License.
|
||||
You may obtain a copy of the License at
|
||||
|
||||
http://www.apache.org/licenses/LICENSE-2.0
|
||||
|
||||
Unless required by applicable law or agreed to in writing, software
|
||||
distributed under the License is distributed on an "AS IS" BASIS,
|
||||
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
|
||||
See the License for the specific language governing permissions and
|
||||
limitations under the License.
|
||||
|
|
@ -0,0 +1,4 @@
|
|||
include LICENSE
|
||||
include README.md
|
||||
graft docs
|
||||
graft examples
|
||||
|
|
@ -0,0 +1,82 @@
|
|||
[](https://www.apache.org/licenses/LICENSE-2.0)
|
||||
[](https://python.org)
|
||||
|
||||
## Installation
|
||||
|
||||
### Docker
|
||||
|
||||
```bash
|
||||
git clone https://git.idrl.site/pengwei/idrlnet_public
|
||||
cd idrlnet_public
|
||||
docker build . -t idrlnet_dev
|
||||
docker run -it -p [EXPOSED_SSH_PORT]:22 -v [CURRENT_WORK_DIR]:/root/pinnnet idrlnet_dev:latest bash
|
||||
```
|
||||
|
||||
### Anaconda
|
||||
|
||||
```bash
|
||||
git clone https://git.idrl.site/pengwei/idrlnet_public
|
||||
cd idrlnet_public
|
||||
conda create -n idrlnet_dev python=3.8 -y
|
||||
conda activate idrlnet_dev
|
||||
pip install -r requirements.txt
|
||||
pip install -e .
|
||||
```
|
||||
|
||||
# IDRLnet
|
||||
|
||||
IDRLnet is a machine learning library on top of [Pytorch](https://www.tensorflow.org/). Use IDRLnet if you need a machine
|
||||
learning library that solves both forward and inverse partial differential equations (PDEs) via physics-informed neural
|
||||
networks (PINN). IDRLnet is a flexible framework inspired by [Nvidia Simnet](https://developer.nvidia.com/simnet>).
|
||||
|
||||
## Features
|
||||
|
||||
IDRLnet supports
|
||||
|
||||
- complex domain geometries without mesh generation. Provided geometries include interval, triangle, rectangle, polygon,
|
||||
circle, sphere... Other geometries can be constructed using three boolean operations: union, difference, and
|
||||
intersection;
|
||||
|
||||
- sampling in the interior of the defined geometry or on the boundary with given conditions.
|
||||
|
||||
- enables the user code to be structured. Data sources, operations, constraints are all represented by ``Node``. The graph
|
||||
will be automatically constructed via label symbols of each node. Getting rid of the explicit construction via
|
||||
explicit expressions, users model problems more naturally.
|
||||
|
||||
- solving variational minimization problem;
|
||||
|
||||
- solving integral differential equation;
|
||||
|
||||
- adaptive resampling;
|
||||
|
||||
- recover unknown parameters of PDEs from noisy measurement data.
|
||||
|
||||
It is also easy to customize IDRLnet to meet new demands.
|
||||
|
||||
- Main Dependencies
|
||||
|
||||
- [Matplotlib](https://matplotlib.org/)
|
||||
- [NumPy](http://www.numpy.org/)
|
||||
- [Sympy](https://https://www.sympy.org/)==1.5.1
|
||||
- [pytorch](https://www.tensorflow.org/)>=1.7.0
|
||||
|
||||
## Contributing to IDRLnet
|
||||
|
||||
First off, thanks for taking the time to contribute!
|
||||
|
||||
- **Reporting bugs.** To report a bug, simply open an issue in the GitHub "Issues" section.
|
||||
|
||||
- **Suggesting enhancements.** To submit an enhancement suggestion for IDRLnet, including completely new features and
|
||||
minor improvements to existing functionality, let us know by opening an issue.
|
||||
|
||||
- **Pull requests.** If you made improvements to IDRLnet, fixed a bug, or had a new example, feel free to send us a
|
||||
pull-request.
|
||||
|
||||
- **Asking questions.** To get help on how to use IDRLnet or its functionalities, you can as well open an issue.
|
||||
|
||||
- **Answering questions.** If you know the answer to any question in the "Issues", you are welcomed to answer.
|
||||
|
||||
## The Team
|
||||
|
||||
IDRLnet was originally developed by IDRL lab.
|
||||
|
||||
|
|
@ -0,0 +1,20 @@
|
|||
# Minimal makefile for Sphinx documentation
|
||||
#
|
||||
|
||||
# You can set these variables from the command line, and also
|
||||
# from the environment for the first two.
|
||||
SPHINXOPTS ?=
|
||||
SPHINXBUILD ?= sphinx-build
|
||||
SOURCEDIR = .
|
||||
BUILDDIR = _build
|
||||
|
||||
# Put it first so that "make" without argument is like "make help".
|
||||
help:
|
||||
@$(SPHINXBUILD) -M help "$(SOURCEDIR)" "$(BUILDDIR)" $(SPHINXOPTS) $(O)
|
||||
|
||||
.PHONY: help Makefile
|
||||
|
||||
# Catch-all target: route all unknown targets to Sphinx using the new
|
||||
# "make mode" option. $(O) is meant as a shortcut for $(SPHINXOPTS).
|
||||
%: Makefile
|
||||
@$(SPHINXBUILD) -M $@ "$(SOURCEDIR)" "$(BUILDDIR)" $(SPHINXOPTS) $(O)
|
||||
|
|
@ -0,0 +1,87 @@
|
|||
# Configuration file for the Sphinx documentation builder.
|
||||
#
|
||||
# This file only contains a selection of the most common options. For a full
|
||||
# list see the documentation:
|
||||
# https://www.sphinx-doc.org/en/master/usage/configuration.html
|
||||
|
||||
# -- Path setup --------------------------------------------------------------
|
||||
|
||||
# If extensions (or modules to document with autodoc) are in another directory,
|
||||
# add these directories to sys.path here. If the directory is relative to the
|
||||
# documentation root, use os.path.abspath to make it absolute, like shown here.
|
||||
#
|
||||
import os
|
||||
import sys
|
||||
|
||||
sys.path.insert(0, os.path.abspath('..'))
|
||||
|
||||
# -- Project information -----------------------------------------------------
|
||||
|
||||
project = 'idrlnet'
|
||||
copyright = '2021, IDRL'
|
||||
author = 'IDRL'
|
||||
|
||||
# The full version, including alpha/beta/rc tags
|
||||
release = '1.0.4'
|
||||
|
||||
# -- General configuration ---------------------------------------------------
|
||||
|
||||
# Add any Sphinx extension module names here, as strings. They can be
|
||||
# extensions coming with Sphinx (named 'sphinx.ext.*') or your custom
|
||||
# ones.
|
||||
extensions = [
|
||||
"sphinx.ext.autodoc",
|
||||
"sphinx.ext.mathjax",
|
||||
"sphinx.ext.napoleon",
|
||||
"sphinx.ext.viewcode",
|
||||
'myst_parser',
|
||||
'sphinx.ext.autosectionlabel',
|
||||
]
|
||||
|
||||
# Add any paths that contain templates here, relative to this directory.
|
||||
templates_path = ['_templates']
|
||||
|
||||
source_suffix = {
|
||||
'.rst': 'restructuredtext',
|
||||
'.txt': 'markdown',
|
||||
'.md': 'markdown',
|
||||
}
|
||||
# List of patterns, relative to source directory, that match files and
|
||||
# directories to ignore when looking for source files.
|
||||
# This pattern also affects html_static_path and html_extra_path.
|
||||
exclude_patterns = ['_build', 'Thumbs.db', '.DS_Store']
|
||||
|
||||
# -- Options for HTML output -------------------------------------------------
|
||||
|
||||
# The theme to use for HTML and HTML Help pages. See the documentation for
|
||||
# a list of builtin themes.
|
||||
#
|
||||
html_theme = 'sphinx_rtd_theme'
|
||||
|
||||
# Add any paths that contain custom static files (such as style sheets) here,
|
||||
# relative to this directory. They are copied after the builtin static files,
|
||||
# so a file named "default.css" will overwrite the builtin "default.css".
|
||||
html_static_path = ['_static']
|
||||
|
||||
# for MarkdownParser
|
||||
from sphinx_markdown_parser.parser import MarkdownParser
|
||||
|
||||
|
||||
# def setup(app):
|
||||
# # app.add_source_suffix('.md', 'markdown')
|
||||
# # app.add_source_parser(MarkdownParser)
|
||||
# app.add_config_value('markdown_parser_config', {
|
||||
# 'auto_toc_tree_section': 'Content',
|
||||
# 'enable_auto_doc_ref': True,
|
||||
# 'enable_auto_toc_tree': True,
|
||||
# 'enable_eval_rst': True,
|
||||
# 'extensions': [
|
||||
# 'extra',
|
||||
# 'nl2br',
|
||||
# 'sane_lists',
|
||||
# 'smarty',
|
||||
# 'toc',
|
||||
# 'wikilinks',
|
||||
# 'pymdownx.arithmatex',
|
||||
# ],
|
||||
# }, True)
|
||||
|
|
@ -0,0 +1,48 @@
|
|||
Welcome to idrlnet's documentation!
|
||||
===================================
|
||||
|
||||
.. toctree::
|
||||
:maxdepth: 2
|
||||
|
||||
user/installation
|
||||
user/get_started/tutorial
|
||||
user/cite_idrlnet
|
||||
user/team
|
||||
|
||||
Features
|
||||
--------
|
||||
|
||||
IDRLnet is a machine learning library on top of `Pytorch <https://www.tensorflow.org/>`_. Use IDRLnet if you need a machine
|
||||
learning library that solves both forward and inverse partial differential equations (PDEs) via physics-informed neural
|
||||
networks (PINN). IDRLnet is a flexible framework inspired by `Nvidia Simnet <https://developer.nvidia.com/simnet>`_.
|
||||
|
||||
IDRLnet supports
|
||||
|
||||
- complex domain geometries without mesh generation. Provided geometries include interval, triangle, rectangle, polygon,
|
||||
circle, sphere... Other geometries can be constructed using three boolean operations: union, difference, and
|
||||
intersection;
|
||||
- sampling in the interior of the defined geometry or on the boundary with given conditions.
|
||||
- enables the user code to be structured. Data sources, operations, constraints are all represented by ``Node``. The graph
|
||||
will be automatically constructed via label symbols of each node. Getting rid of the explicit construction via
|
||||
explicit expressions, users model problems more naturally.
|
||||
- solving variational minimization problem;
|
||||
- solving integral differential equation;
|
||||
- adaptive resampling;
|
||||
- recover unknown parameter of PDEs from noisy measurement data.
|
||||
|
||||
API reference
|
||||
=============
|
||||
If you are looking for usage of a specific function, class or method, please refer to the following part.
|
||||
|
||||
.. toctree::
|
||||
:maxdepth: 2
|
||||
|
||||
|
||||
modules/modules
|
||||
|
||||
Indices and tables
|
||||
==================
|
||||
|
||||
* :ref:`genindex`
|
||||
* :ref:`modindex`
|
||||
* :ref:`search`
|
||||
|
|
@ -0,0 +1,35 @@
|
|||
@ECHO OFF
|
||||
|
||||
pushd %~dp0
|
||||
|
||||
REM Command file for Sphinx documentation
|
||||
|
||||
if "%SPHINXBUILD%" == "" (
|
||||
set SPHINXBUILD=sphinx-build
|
||||
)
|
||||
set SOURCEDIR=.
|
||||
set BUILDDIR=_build
|
||||
|
||||
if "%1" == "" goto help
|
||||
|
||||
%SPHINXBUILD% >NUL 2>NUL
|
||||
if errorlevel 9009 (
|
||||
echo.
|
||||
echo.The 'sphinx-build' command was not found. Make sure you have Sphinx
|
||||
echo.installed, then set the SPHINXBUILD environment variable to point
|
||||
echo.to the full path of the 'sphinx-build' executable. Alternatively you
|
||||
echo.may add the Sphinx directory to PATH.
|
||||
echo.
|
||||
echo.If you don't have Sphinx installed, grab it from
|
||||
echo.http://sphinx-doc.org/
|
||||
exit /b 1
|
||||
)
|
||||
|
||||
%SPHINXBUILD% -M %1 %SOURCEDIR% %BUILDDIR% %SPHINXOPTS% %O%
|
||||
goto end
|
||||
|
||||
:help
|
||||
%SPHINXBUILD% -M help %SOURCEDIR% %BUILDDIR% %SPHINXOPTS% %O%
|
||||
|
||||
:end
|
||||
popd
|
||||
|
|
@ -0,0 +1,34 @@
|
|||
idrlnet.architecture package
|
||||
============================
|
||||
|
||||
.. automodule:: idrlnet.architecture
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
Submodules
|
||||
----------
|
||||
|
||||
idrlnet.architecture.grid module
|
||||
--------------------------------
|
||||
|
||||
.. automodule:: idrlnet.architecture.grid
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.architecture.layer module
|
||||
---------------------------------
|
||||
|
||||
.. automodule:: idrlnet.architecture.layer
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.architecture.mlp module
|
||||
-------------------------------
|
||||
|
||||
.. automodule:: idrlnet.architecture.mlp
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
|
@ -0,0 +1,42 @@
|
|||
idrlnet.geo\_utils package
|
||||
==========================
|
||||
|
||||
.. automodule:: idrlnet.geo_utils
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
Submodules
|
||||
----------
|
||||
|
||||
idrlnet.geo\_utils.geo module
|
||||
-----------------------------
|
||||
|
||||
.. automodule:: idrlnet.geo_utils.geo
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.geo\_utils.geo\_builder module
|
||||
--------------------------------------
|
||||
|
||||
.. automodule:: idrlnet.geo_utils.geo_builder
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.geo\_utils.geo\_obj module
|
||||
----------------------------------
|
||||
|
||||
.. automodule:: idrlnet.geo_utils.geo_obj
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.geo\_utils.sympy\_np module
|
||||
-----------------------------------
|
||||
|
||||
.. automodule:: idrlnet.geo_utils.sympy_np
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
|
@ -0,0 +1,26 @@
|
|||
idrlnet.pde\_op package
|
||||
=======================
|
||||
|
||||
.. automodule:: idrlnet.pde_op
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
Submodules
|
||||
----------
|
||||
|
||||
idrlnet.pde\_op.equations module
|
||||
--------------------------------
|
||||
|
||||
.. automodule:: idrlnet.pde_op.equations
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.pde\_op.operator module
|
||||
-------------------------------
|
||||
|
||||
.. automodule:: idrlnet.pde_op.operator
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
|
@ -0,0 +1,124 @@
|
|||
idrlnet package
|
||||
===============
|
||||
|
||||
.. automodule:: idrlnet
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
Subpackages
|
||||
-----------
|
||||
|
||||
.. toctree::
|
||||
:maxdepth: 4
|
||||
|
||||
idrlnet.architecture
|
||||
idrlnet.geo_utils
|
||||
idrlnet.pde_op
|
||||
|
||||
Submodules
|
||||
----------
|
||||
|
||||
idrlnet.callbacks module
|
||||
------------------------
|
||||
|
||||
.. automodule:: idrlnet.callbacks
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.data module
|
||||
-------------------
|
||||
|
||||
.. automodule:: idrlnet.data
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.graph module
|
||||
--------------------
|
||||
|
||||
.. automodule:: idrlnet.graph
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.header module
|
||||
---------------------
|
||||
|
||||
.. automodule:: idrlnet.header
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.net module
|
||||
------------------
|
||||
|
||||
.. automodule:: idrlnet.net
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.node module
|
||||
-------------------
|
||||
|
||||
.. automodule:: idrlnet.node
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.optim module
|
||||
--------------------
|
||||
|
||||
.. automodule:: idrlnet.optim
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.pde module
|
||||
------------------
|
||||
|
||||
.. automodule:: idrlnet.pde
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.receivers module
|
||||
------------------------
|
||||
|
||||
.. automodule:: idrlnet.receivers
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.shortcut module
|
||||
-----------------------
|
||||
|
||||
.. automodule:: idrlnet.shortcut
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.solver module
|
||||
---------------------
|
||||
|
||||
.. automodule:: idrlnet.solver
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.torch\_util module
|
||||
--------------------------
|
||||
|
||||
.. automodule:: idrlnet.torch_util
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
||||
idrlnet.variable module
|
||||
-----------------------
|
||||
|
||||
.. automodule:: idrlnet.variable
|
||||
:members:
|
||||
:undoc-members:
|
||||
:show-inheritance:
|
||||
|
|
@ -0,0 +1,7 @@
|
|||
idrlnet
|
||||
=======
|
||||
|
||||
.. toctree::
|
||||
:maxdepth: 4
|
||||
|
||||
idrlnet
|
||||
|
|
@ -0,0 +1,2 @@
|
|||
# Cite IDRLnet
|
||||
The paper is to appear on Arxiv.
|
||||
|
|
@ -0,0 +1,231 @@
|
|||
# Solving Simple Poisson Equation
|
||||
|
||||
Inspired by [Nvidia SimNet](https://developer.nvidia.com/simnet),
|
||||
IDRLnet employs symbolic links to construct a computational graph automatically.
|
||||
In this section, we introduce the primary usage of IDRLnet.
|
||||
To solve PINN via IDRLnet, we divide the procedure into several parts:
|
||||
|
||||
1. Define symbols and parameters.
|
||||
1. Define geometry objects.
|
||||
1. Define sampling domains and corresponding constraints.
|
||||
1. Define neural networks and PDEs.
|
||||
1. Define solver and solve.
|
||||
1. Post processing.
|
||||
|
||||
We provide the following example to illustrate the primary usages and features of IDRLnet.
|
||||
|
||||
Consider the 2d Poisson's equation defined on $\Omega=[-1,1]\times[-1,1]$, which satisfies $-\Delta u=1$, with
|
||||
the boundary value conditions:
|
||||
|
||||
$$
|
||||
\begin{align}
|
||||
\frac{\partial u(x, -1)}{\partial n}&=\frac{\partial u(x, 1)}{\partial n}=0 \\
|
||||
u(-1,y)&=u(1, y)=0
|
||||
\end{align}
|
||||
$$
|
||||
|
||||
## Define Symbols
|
||||
For the 2d problem, we define two coordinate symbols `x` and `y`, which will be used in symbolic expressions in IDRLnet.
|
||||
```python
|
||||
x, y = sp.symbols('x y')
|
||||
```
|
||||
Note that variables `x`, `y`, `z`, `t` are reserved inside IDRLnet.
|
||||
The four symbols should only represent the 4 primary coordinates.
|
||||
|
||||
## Define Geometric Objects
|
||||
|
||||
The geometry object is a simple rectangle.
|
||||
```python
|
||||
rec = sc.Rectangle((-1., -1.), (1., 1.))
|
||||
```
|
||||
|
||||
Users can sample points on these geometry objects. The operators `+`, `-`, `&` are also supported.
|
||||
A slightly more complicated example is as follows:
|
||||
```python
|
||||
import numpy as np
|
||||
import idrlnet.shortcut as sc
|
||||
|
||||
# Define 4 polygons
|
||||
I = sc.Polygon([(0, 0), (3, 0), (3, 1), (2, 1), (2, 4), (3, 4), (3, 5), (0, 5), (0, 4), (1, 4), (1, 1), (0, 1)])
|
||||
D = sc.Polygon([(4, 0), (7, 0), (8, 1), (8, 4), (7, 5), (4, 5)]) - sc.Polygon(([5, 1], [7, 1], [7, 4], [5, 4]))
|
||||
R = sc.Polygon([(9, 0), (10, 0), (10, 2), (11, 2), (12, 0), (13, 0), (12, 2), (13, 3), (13, 4), (12, 5), (9, 5)]) \
|
||||
- sc.Rectangle(point_1=(10., 3.), point_2=(12, 4))
|
||||
L = sc.Polygon([(14, 0), (17, 0), (17, 1), (15, 1), (15, 5), (14, 5)])
|
||||
|
||||
# Define a heart shape.
|
||||
heart = sc.Heart((18, 4), radius=1)
|
||||
|
||||
# Union of the 5 geometry objects
|
||||
geo = (I + D + R + L + heart)
|
||||
|
||||
# interior samples
|
||||
points = geo.sample_interior(density=100, low_discrepancy=True)
|
||||
plt.figure(figsize=(10, 5))
|
||||
plt.scatter(x=points['x'], y=points['y'], c=points['sdf'], cmap='hot')
|
||||
|
||||
# boundary samples
|
||||
points = geo.sample_boundary(density=400, low_discrepancy=True)
|
||||
plt.scatter(x=points['x'], y=points['y'])
|
||||
idx = np.random.choice(points['x'].shape[0], 400, replace=False)
|
||||
|
||||
# Show normal directions on boundary
|
||||
plt.quiver(points['x'][idx], points['y'][idx], points['normal_x'][idx], points['normal_y'][idx])
|
||||
plt.show()
|
||||
```
|
||||
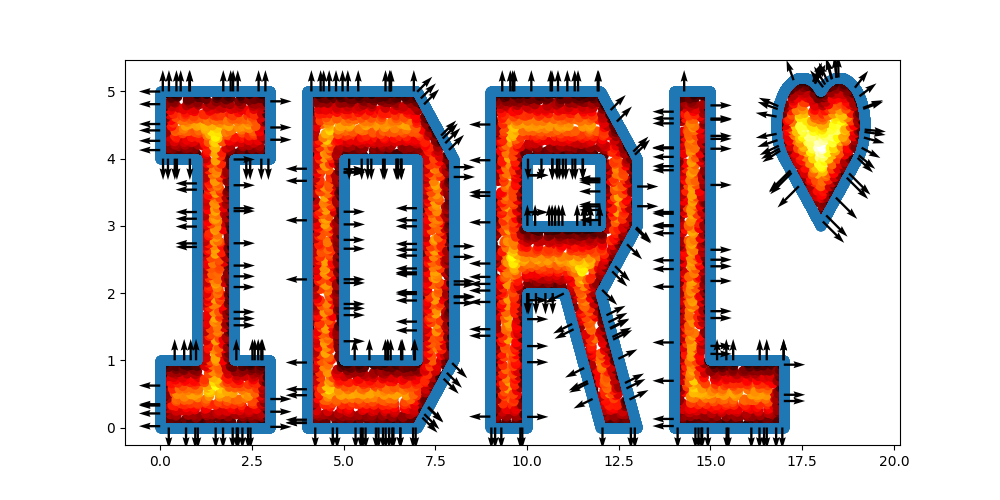
|
||||
|
||||
## Define Sampling Methods and Constraints
|
||||
Take a 1D fitting task as an example.
|
||||
The data source generates pairs $(x_i, f_i)$. We train a network $u_\theta(x_i)\approx f_i$.
|
||||
Then $f_i$ is the target output of $u_\theta(x_i)$.
|
||||
These targets are called constraints in IDRLnet.
|
||||
|
||||
For the problem, three constraints are presented.
|
||||
|
||||
The constraint
|
||||
|
||||
$$
|
||||
u(-1,y)=u(1, y)=0
|
||||
$$
|
||||
is translated into
|
||||
```python
|
||||
@sc.datanode
|
||||
class LeftRight(sc.SampleDomain):
|
||||
# Due to `name` is not specified, LeftRight will be the name of datanode automatically
|
||||
def sampling(self, *args, **kwargs):
|
||||
# sieve define rules to filter points
|
||||
points = rec.sample_boundary(1000, sieve=((y > -1.) & (y < 1.)))
|
||||
constraints = sc.Variables({'T': 0.})
|
||||
return points, constraints
|
||||
```
|
||||
Then `LeftRight()` is wrapped as an instance of `DataNode`.
|
||||
One can store states in these instances.
|
||||
Alternatively, if users do not need storing states, the code above is equivalent to
|
||||
```python
|
||||
@sc.datanode(name='LeftRight')
|
||||
def leftright(self, *args, **kwargs):
|
||||
points = rec.sample_boundary(1000, sieve=((y > -1.) & (y < 1.)))
|
||||
constraints = sc.Variables({'T': 0.})
|
||||
return points, constraints
|
||||
```
|
||||
Then `sampling()` is wrapped as an instance of `DataNode`.
|
||||
|
||||
The constraint
|
||||
|
||||
$$
|
||||
\frac{\partial u(x, -1)}{\partial n}=\frac{\partial u(x, 1)}{\partial n}=0
|
||||
$$
|
||||
is translated into
|
||||
|
||||
```python
|
||||
@sc.datanode(name="up_down")
|
||||
class UpDownBoundaryDomain(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_boundary(1000, sieve=((x > -1.) & (x < 1.)))
|
||||
constraints = sc.Variables({'normal_gradient_T': 0.})
|
||||
return points, constraints
|
||||
```
|
||||
The constraint `normal_gradient_T` will also be one of the output of computable nodes, including `PdeNode` or `NetNode`.
|
||||
|
||||
The last constraint is the PDE itself $-\Delta u=1$:
|
||||
|
||||
```python
|
||||
@sc.datanode(name="heat_domain")
|
||||
class HeatDomain(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
self.points = 1000
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_interior(self.points)
|
||||
constraints = sc.Variables({'diffusion_T': 1.})
|
||||
return points, constraints
|
||||
```
|
||||
`diffusion_T` will also be one of the outputs of computable nodes.
|
||||
`self.points` is a stored state and can be varied to control the sampling behaviors.
|
||||
|
||||
## Define Neural Networks and PDEs
|
||||
As mentioned before, neural networks and PDE expressions are encapsulated as `Node` too.
|
||||
The `Node` objects have `inputs`, `derivatives`, `outputs` properties and the `evaluate()` method.
|
||||
According to their inputs, derivatives, and outputs, these nodes will be automatically connected as a computational graph.
|
||||
A topological sort will be applied to the graph to decide the computation order.
|
||||
|
||||
```python
|
||||
net = sc.get_net_node(inputs=('x', 'y',), outputs=('T',), name='net1', arch=sc.Arch.mlp)
|
||||
```
|
||||
This is a simple call to get a neural network with the predefined architecture.
|
||||
As an alternative, one can specify the configurations via
|
||||
```python
|
||||
evaluate = MLP(n_seq=[2, 20, 20, 20, 20, 1)],
|
||||
activation=Activation.swish,
|
||||
initialization=Initializer.kaiming_uniform,
|
||||
weight_norm=True)
|
||||
net = NetNode(inputs=('x', 'y',), outputs=('T',), net=evaluate, name='net1', *args, **kwargs)
|
||||
```
|
||||
which generates a node with
|
||||
- `inputs=('x','y')`,
|
||||
- `derivatives=tuple()`,
|
||||
- `outpus=('T')`
|
||||
```python
|
||||
pde = sc.DiffusionNode(T='T', D=1., Q=0., dim=2, time=False)
|
||||
```
|
||||
generates a node with
|
||||
- `inputs=tuple()`,
|
||||
- `derivatives=('T__x', 'T__y')`,
|
||||
- `outputs=('diffusion_T',)`.
|
||||
|
||||
```python
|
||||
grad = sc.NormalGradient('T', dim=2, time=False)
|
||||
```
|
||||
generates a node with
|
||||
- `inputs=('normal_x', 'normal_y')`,
|
||||
- `derivatives=('T__x', 'T__y')`,
|
||||
- `outputs=('normal_gradient_T',)`.
|
||||
The string `__` is reserved to represent the derivative operator.
|
||||
If the required derivatives cannot be directly obtained from outputs of other nodes,
|
||||
It will try `autograd` provided by Pytorch with the maximum prefix match from outputs of other nodes.
|
||||
|
||||
## Define A Solver
|
||||
Initialize a solver to bundle all the components and solve the model.
|
||||
```python
|
||||
s = sc.Solver(sample_domains=(HeatDomain(), LeftRight(), UpDownBoundaryDomain()),
|
||||
netnodes=[net],
|
||||
pdes=[pde, grad],
|
||||
max_iter=1000)
|
||||
s.solve()
|
||||
```
|
||||
Before the solver start running, it constructs computational graphs and applies a topological sort to decide the evaluation order.
|
||||
Each sample domain has its independent graph.
|
||||
The procedures will be executed automatically when the solver detects potential changes in graphs.
|
||||
As default, these graphs are also visualized as `png` in the `network` directory named after the corresponding domain.
|
||||
|
||||
The following figure shows the graph on `UpDownBoundaryDomain`:
|
||||
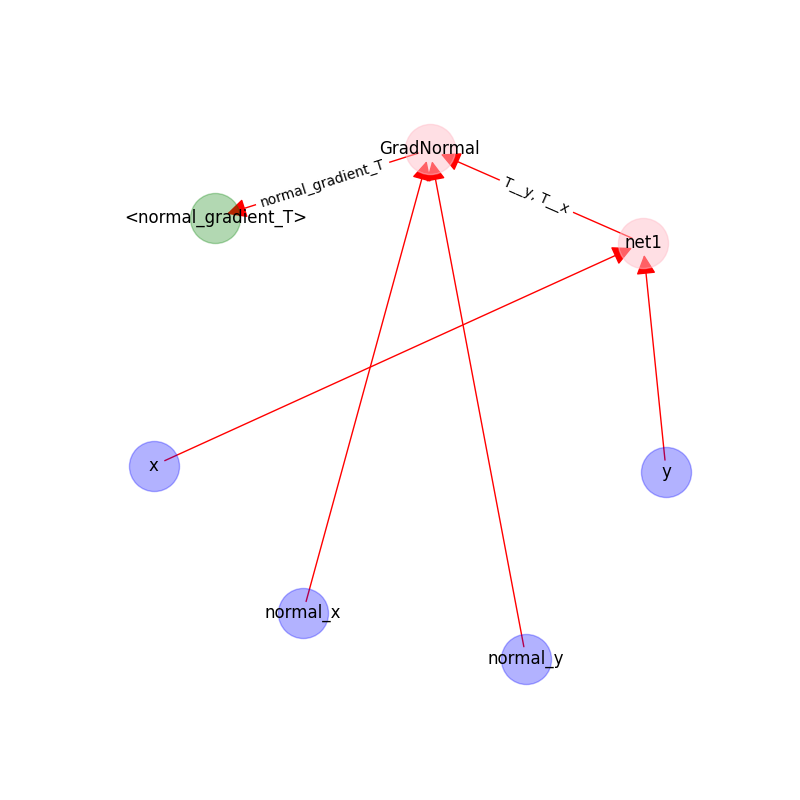
|
||||
|
||||
- The blue nodes are generated via sampling;
|
||||
- the red nodes are computational;
|
||||
- the green nodes are constraints(targets).
|
||||
|
||||
## Inference
|
||||
We use domain `heat_domain` for inference.
|
||||
First, we increase the density to 10000 via changing the attributes of the domain.
|
||||
Then, `Solver.infer_step()` is called for inference.
|
||||
```python
|
||||
s.set_domain_parameter('heat_domain', {'points': 10000})
|
||||
coord = s.infer_step({'heat_domain': ['x', 'y', 'T']})
|
||||
num_x = coord['heat_domain']['x'].cpu().detach().numpy().ravel()
|
||||
num_y = coord['heat_domain']['y'].cpu().detach().numpy().ravel()
|
||||
num_Tp = coord['heat_domain']['T'].cpu().detach().numpy().ravel()
|
||||
```
|
||||
|
||||
One may also define a separate domain for inference, which generates `constraints={}`, and thus, no computational graphs will be generated on the domain.
|
||||
We will see this later.
|
||||
|
||||
## Performance Issues
|
||||
1. When a domain is contained by `Solver.sample_domains`, the `sampling()` will be called every iteration.
|
||||
Users should avoid including redundant domains.
|
||||
Future versions will ignore domains with `constraints={}` in training steps.
|
||||
2. The current version samples points in memory.
|
||||
When GPU devices are enabled, data exchange between the memory and GPU devices might hinder the performance.
|
||||
In future versions, we will sample points directly in GPU devices if available.
|
||||
|
||||
See `examples/simple_poisson`.
|
||||
|
|
@ -0,0 +1,72 @@
|
|||
# Euler–Bernoulli beam
|
||||
We consider the Euler–Bernoulli beam equation,
|
||||
|
||||
$$
|
||||
\begin{align}
|
||||
\frac{\partial^{2}}{\partial x^{2}}\left(\frac{\partial^{2} u}{\partial x^{2}}\right)=-1 \\
|
||||
u|_{x=0}=0, u^{\prime}|_{x=0}=0, \\
|
||||
u^{\prime \prime}|_{x=1}=0, u^{\prime \prime \prime}|_{x=1}=0,
|
||||
\end{align}
|
||||
$$
|
||||
which models the following beam with external forces.
|
||||
|
||||
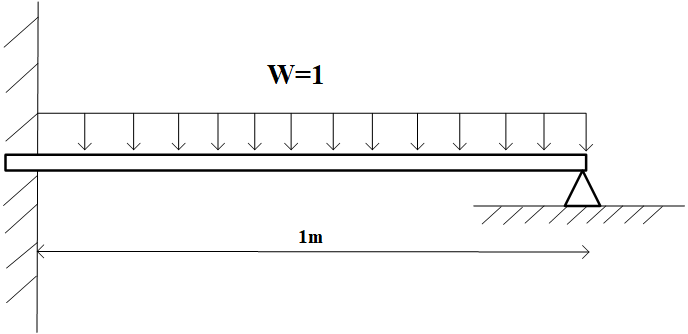
|
||||
|
||||
## Expression Node
|
||||
The Euler-Bernoulli beam equation is not implemented inside IDRLnet.
|
||||
Users may add the equation to `idrlnet.pde_op.equations`.
|
||||
However, one may also define the differential equation via symbol expressions directly.
|
||||
|
||||
First, we define a function symbol in the symbol definition part.
|
||||
```python
|
||||
x = sp.symbols('x')
|
||||
y = sp.Function('y')(x)
|
||||
```
|
||||
In the PDE definition part, we add these PDE nodes:
|
||||
|
||||
```python
|
||||
pde1 = sc.ExpressionNode(name='dddd_y', expression=y.diff(x).diff(x).diff(x).diff(x) + 1)
|
||||
pde2 = sc.ExpressionNode(name='d_y', expression=y.diff(x))
|
||||
pde3 = sc.ExpressionNode(name='dd_y', expression=y.diff(x).diff(x))
|
||||
pde4 = sc.ExpressionNode(name='ddd_y', expression=y.diff(x).diff(x).diff(x))
|
||||
```
|
||||
These are instances of `idrl.pde.PdeNode`, which are also computational nodes.
|
||||
For example, `pde1` is an instance of `Node` with
|
||||
- `inputs=tuple()`;
|
||||
- `derivatives=(y__x__x__x__x, )`;
|
||||
- `outputs=('dddd_y',)`.
|
||||
|
||||
The four PDE nodes match the following operators, respectively:
|
||||
- $dy^4/d^4x+1$;
|
||||
- $dy/dx$;
|
||||
- $dy^2/d^2x$;
|
||||
- $dy^3/d^3x$.
|
||||
|
||||
## Seperate Inference Domain
|
||||
In this example, we define a domain specified for inference.
|
||||
```python
|
||||
@sc.datanode(name='infer')
|
||||
class Infer(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
return {'x': np.linspace(0, 1, 1000).reshape(-1, 1)}, {}
|
||||
```
|
||||
Its instance is not be passed to the solver initializer,
|
||||
which may improve the performance since Infer().sampling
|
||||
After the solving procedure ends, we change the `sample_domains` of the solver,
|
||||
|
||||
```python
|
||||
solver.sample_domains = (Infer(),)
|
||||
```
|
||||
which triggers the regeneration of the computational graph. Then `solver.infer_step()` is called.
|
||||
|
||||
```python
|
||||
points = solver.infer_step({'infer': ['x', 'y']})
|
||||
xs = points['infer']['x'].detach().cpu().numpy().ravel()
|
||||
y_pred = points['infer']['y'].detach().cpu().numpy().ravel()
|
||||
```
|
||||
|
||||
The result is shown as follows.
|
||||
|
||||
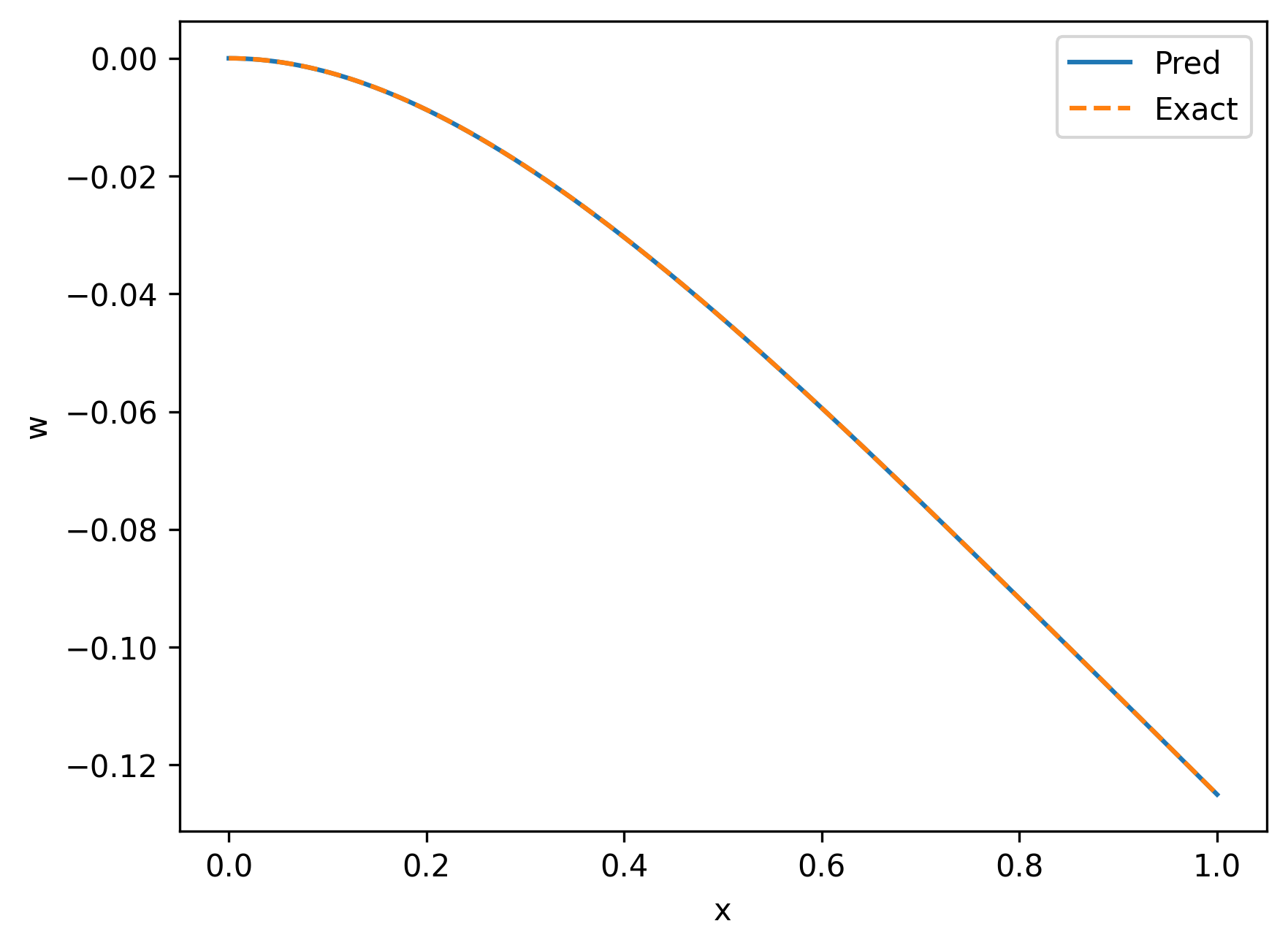
|
||||
|
||||
See `examples/euler_beam`.
|
||||
|
|
@ -0,0 +1,58 @@
|
|||
# Burgers' Equation
|
||||
Burgers' equation is formulated as following:
|
||||
|
||||
$$
|
||||
\begin{equation}
|
||||
\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=\nu \frac{\partial^{2} u}{\partial x^{2}}
|
||||
\end{equation}
|
||||
$$
|
||||
We have added the template of the equation into `idrlnet.pde_op.equations`.
|
||||
In this example, we take $\nu=-0.01/\pi$, and the problem is
|
||||
|
||||
$$
|
||||
\begin{equation}
|
||||
\begin{array}{l}
|
||||
u_t+u u_{x}-(0.01 / \pi) u_{x x}=0, \quad x \in[-1,1], \quad t \in[0,1] \\
|
||||
u(0, x)=-\sin (\pi x) \\
|
||||
u(t,-1)=u(t, 1)=0
|
||||
\end{array}
|
||||
\end{equation}.
|
||||
$$
|
||||
|
||||
## Time-dependent Domain
|
||||
The equation is time-dependent. In addition, we define a time symbol `t` and its range.
|
||||
```python
|
||||
t_symbol = Symbol('t')
|
||||
time_range = {t_symbol: (0, 1)}
|
||||
```
|
||||
The parameter range `time_range` will be passed to methods `geo.Geometry.sample_interior()` and `geo.Geometry.sample_boundary()`.
|
||||
The sampling methods generate samples containing the additional dims provided in `param_ranges.keys()`.
|
||||
```python
|
||||
# Interior domain
|
||||
points = geo.sample_interior(10000, bounds={x: (-1., 1.)}, param_ranges=time_range)
|
||||
|
||||
# Initial value condition
|
||||
points = geo.sample_interior(100, param_ranges={t_symbol: 0.0})
|
||||
|
||||
# Boundary condition
|
||||
points = geo.sample_boundary(100, param_ranges=time_range)
|
||||
```
|
||||
|
||||
The result is shown as follows:
|
||||
|
||||
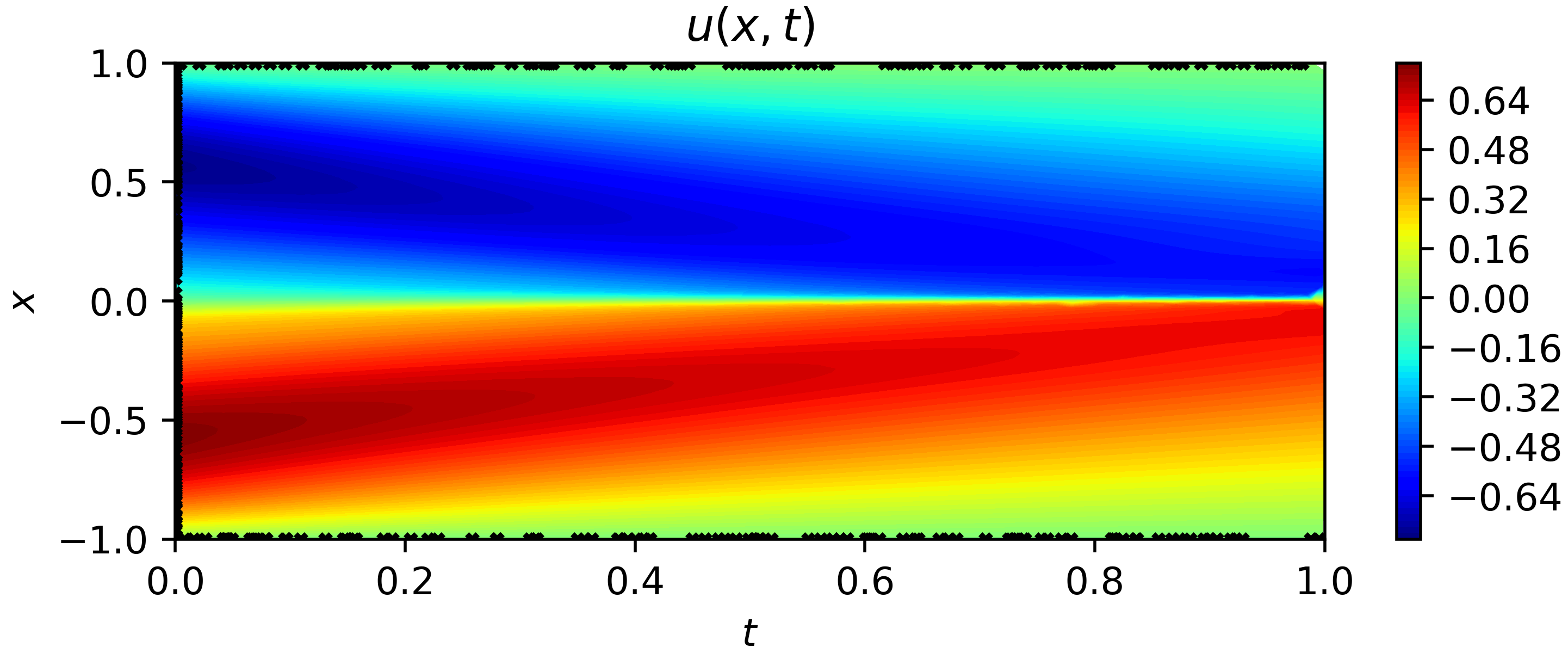
|
||||
|
||||
## Use TensorBoard
|
||||
To monitor the training process, we employ [TensorBoard](https://www.tensorflow.org/tensorboard).
|
||||
The learning rate, losses on different domains, and the total loss will be recorded automatically.
|
||||
Users can call `Solver.summary_receiver()` to get the instance of `SummaryWriter`.
|
||||
As default, one starts TensorBoard at `./network_idr`:
|
||||
```bash
|
||||
tensorboard --logdir ./network_dir
|
||||
```
|
||||
Users can monitor the status of training:
|
||||
|
||||
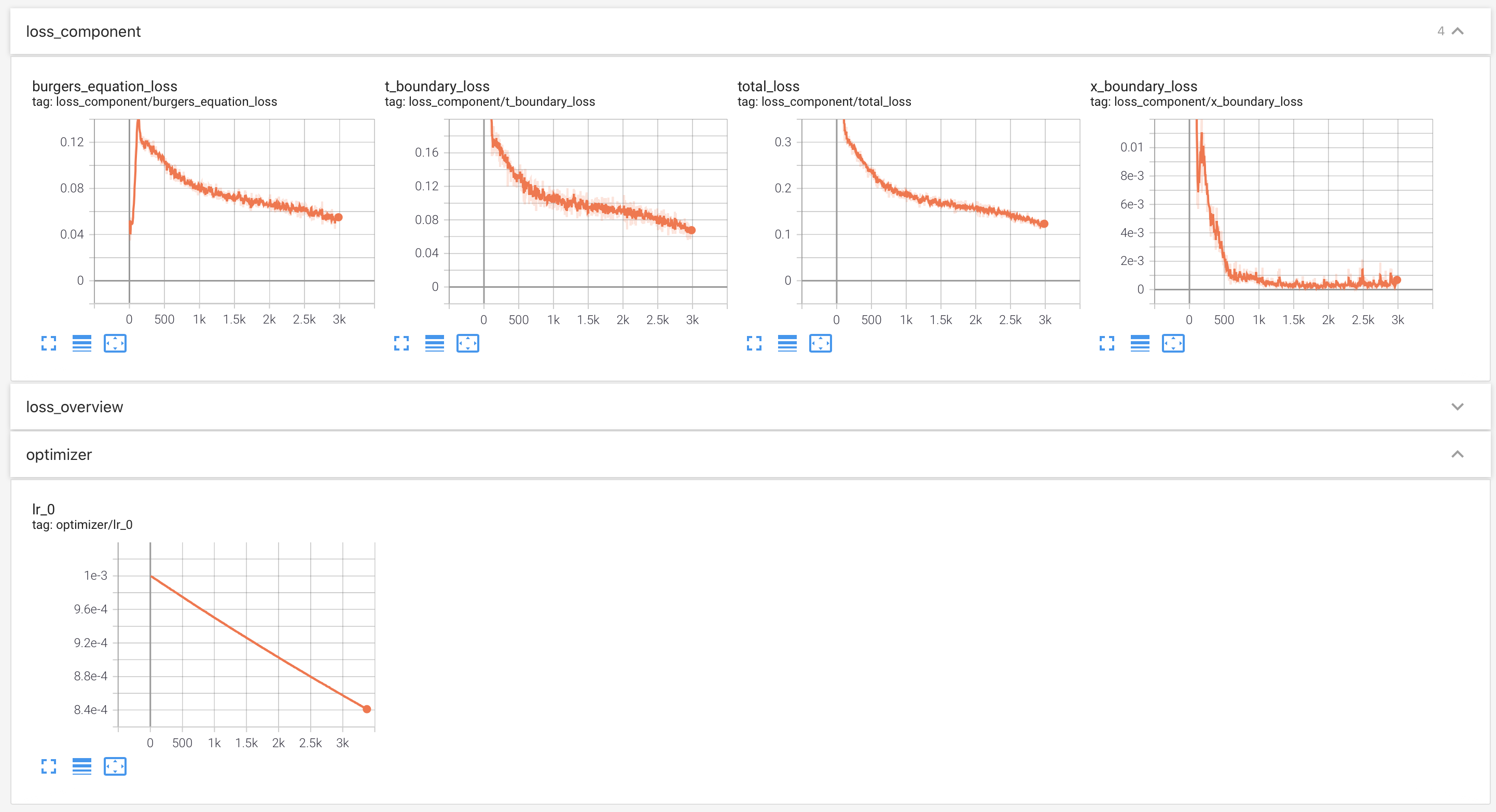
|
||||
|
||||
|
||||
See `examples/burgers_equation`.
|
||||
|
|
@ -0,0 +1,110 @@
|
|||
# Allen-Cahn Equation
|
||||
|
||||
This section repeats the adaptive PINN method presented by [Wight and Zhao][1].
|
||||
|
||||
The Allen-Cahn equation has the following general form:
|
||||
|
||||
$$ \partial_{t} u=\gamma_{1} \Delta u+\gamma_{2}\left(u-u^{3}\right). $$
|
||||
|
||||
Consider the one-dimensional Allen-Cahn equation with periodic boundary conditions:
|
||||
|
||||
$$
|
||||
\begin{array}{l}
|
||||
u_{t}-0.0001 u_{x x}+5 u^{3}-5 u=0, \quad x \in[-1,1], \quad t \in[0,1], \\
|
||||
u(0, x)=x^{2} \cos (\pi x) \\
|
||||
u(t,-1)=u(t, 1) \\
|
||||
u_{x}(t,-1)=u_{x}(t, 1).
|
||||
\end{array}
|
||||
$$
|
||||
|
||||
## Periodic Boundary Conditions
|
||||
|
||||
The periodic boundary conditions are enforced by $u(t, x)=u(t,x+2)$ and $u_x(t, x)=u_x(t,x+2)$ with $x=-1$, which is
|
||||
equivalent to
|
||||
|
||||
$$
|
||||
\begin{array}{l}
|
||||
\tilde u(t,x)=u(t,x+2), \quad \forall t\in[0,1],x\in[-1,1], \\
|
||||
\tilde u(t,x)=u(t,x),\quad \forall t\in[0,1],x=-1, \\
|
||||
\tilde u_x(t,x)=u_x(t,x),\quad \forall t\in[0,1],x=-1.\\
|
||||
\end{array}
|
||||
$$
|
||||
|
||||
The transform above is implemented by
|
||||
|
||||
```python
|
||||
net_u = sc.MLP([2, 128, 128, 128, 128, 2], activation=sc.Activation.tanh)
|
||||
net_u = sc.NetNode(inputs=('x', 't',), outputs=('u',), name='net1', net=net_u)
|
||||
xp = sc.ExpressionNode(name='xp', expression=x + 2)
|
||||
net_tilde_u = sc.get_shared_net_node(net_u, inputs=('xp', 't',), outputs=('up',), name='net2', arch='mlp')
|
||||
```
|
||||
|
||||
where `xp` translates $x$ to $x+2$. The node `net_tilde_u` has the same internal parameters as `net_u` while its inputs
|
||||
and outputs are translated.
|
||||
|
||||
## Receivers acting as Callbacks
|
||||
We define a group of `Signal` to trigger receivers.
|
||||
They are adequate for customizing various PINN algorithms at the moment.
|
||||
|
||||
```python
|
||||
class Signal(Enum):
|
||||
REGISTER = 'signal_register'
|
||||
SOLVE_START = 'signal_solve_start'
|
||||
TRAIN_PIPE_START = 'signal_train_pipe_start'
|
||||
AFTER_COMPUTE_LOSS = 'compute_loss'
|
||||
BEFORE_BACKWARD = 'signal_before_backward'
|
||||
TRAIN_PIPE_END = 'signal_train_pipe_end'
|
||||
SOLVE_END = 'signal_solve_end'
|
||||
```
|
||||
|
||||
We implement the adaptive sampling method as follows.
|
||||
```python
|
||||
class SpaceAdaptiveReceiver(sc.Receiver):
|
||||
# implement the abstract method in sc.Receiver
|
||||
def receive_notify(self, solver, message):
|
||||
# In each iteration, after the train pipe ends, the receiver will be notified.
|
||||
# Every five 500 iterations, the adaptive sampling will be triggerd.
|
||||
if sc.Signal.TRAIN_PIPE_END in message.keys() and solver.global_step % 1000 == 0:
|
||||
sc.logger.info('space adaptive sampling...')
|
||||
# Do extra sampling and compute the residual
|
||||
results = solver.infer_step({'data_evaluate': ['x', 't', 'sdf', 'AllenCahn_u']})
|
||||
residual_data = results['data_evaluate']['AllenCahn_u'].detach().cpu().numpy().ravel()
|
||||
# Sort the points by residual loss
|
||||
index = np.argsort(-1. * np.abs(residual_data))[:200]
|
||||
_points = {key: values[index].detach().cpu().numpy() for key, values in results['data_evaluate'].items()}
|
||||
_points.pop('AllenCahn_u')
|
||||
_points['area'] = np.zeros_like(_points['sdf']) + (1.0 / 200)
|
||||
# Update the points in the re_samping_domain
|
||||
solver.set_domain_parameter('re_sampling_domain', {'points': _points})
|
||||
```
|
||||
We also draw the result every $1000$ iterations.
|
||||
```python
|
||||
class PostProcessReceiver(Receiver):
|
||||
def receive_notify(self, solver, message):
|
||||
if pinnnet.receivers.Signal.TRAIN_PIPE_END in message.keys() and solver.global_step % 1000 == 1:
|
||||
points = s.infer_step({'allen_test': ['x', 't', 'u']})
|
||||
triang_total = tri.Triangulation(points['allen_test']['t'].detach().cpu().numpy().ravel(),
|
||||
points['allen_test']['x'].detach().cpu().numpy().ravel(), )
|
||||
plt.tricontourf(triang_total, points['allen_test']['u'].detach().cpu().numpy().ravel(), 100)
|
||||
tc_bar = plt.colorbar()
|
||||
tc_bar.ax.tick_params(labelsize=12)
|
||||
plt.xlabel('$t$')
|
||||
plt.ylabel('$x$')
|
||||
plt.title('$u(x,t)$')
|
||||
plt.savefig(f'result_{solver.global_step}.png')
|
||||
plt.show()
|
||||
```
|
||||
Before `Solver.solve()` is called, register the two receivers to the solver:
|
||||
|
||||
```python
|
||||
s.register_receiver(SpaceAdaptiveReceiver())
|
||||
s.register_receiver(PostProcessReceiver())
|
||||
```
|
||||
|
||||
The training process is shown as follows:
|
||||
|
||||
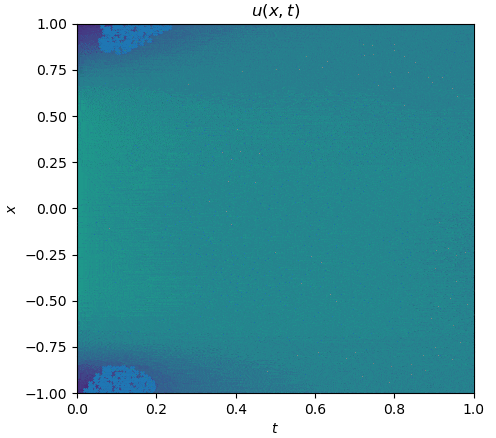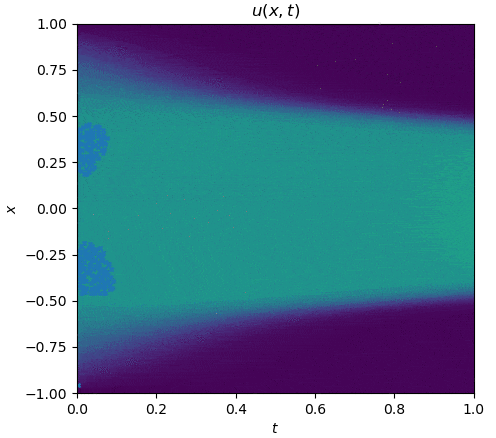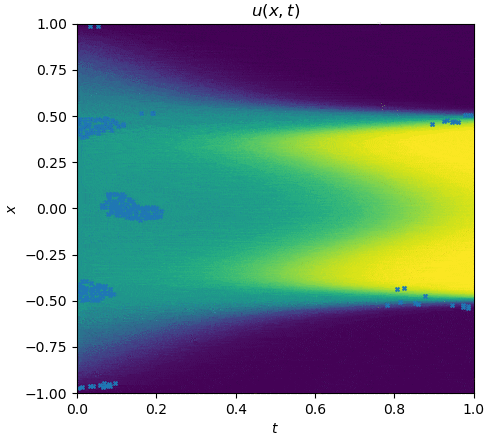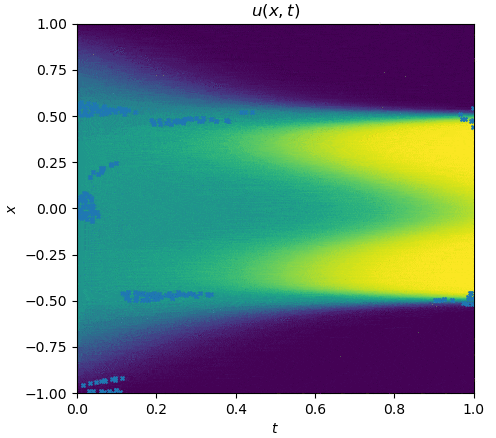
|
||||
|
||||
See `examples/allen_cahn`.
|
||||
|
||||
[1]: <https://arxiv.org/abs/2007.04542>
|
||||
|
|
@ -0,0 +1,94 @@
|
|||
# Inverse Wave Equation
|
||||
Consider the 1d wave equation:
|
||||
|
||||
$$
|
||||
\begin{equation}
|
||||
\frac{\partial^2u}{\partial t^2}=c\frac{\partial^2u}{\partial x^2},
|
||||
\end{equation}
|
||||
$$
|
||||
where $c>0$ is unknown and is to be estimated. A group of data pairs $\{x_i, t_i, u_i\}_{i=1,2,\cdot,N}$ is observed.
|
||||
Then the problem is formulated as:
|
||||
|
||||
$$
|
||||
\min_{u,c} \sum_{i=1,2,\cdots,N} \|u(x_i, t_i)-u_i\|^2\\
|
||||
s.t. \frac{\partial^2u}{\partial t^2}=c\frac{\partial^2u}{\partial x^2}
|
||||
$$
|
||||
|
||||
In the context of PINN, $u$ is parameterized to $u_\theta$.
|
||||
The problem above is transformed to the discrete form:
|
||||
|
||||
$$
|
||||
\min_{\theta,c}
|
||||
w_1\sum_{i=1,2,\cdots,N} \|u_\theta(x_i, t_i)-u_i\|^2
|
||||
+w_2\sum_{i=1,2,\cdots,M}\left|\frac{\partial^2u_\theta(x_i,t_i)}{\partial t^2}-c\frac{\partial^2u_\theta(x_i,t_i)}{\partial x^2}\right|^2.
|
||||
$$
|
||||
|
||||
## Importing External Data
|
||||
We take the ground truth
|
||||
|
||||
$$
|
||||
u=\sin x \cdot(\sin 1.54 t + \cos 1.54 t),
|
||||
$$
|
||||
where $c=1.54$.
|
||||
The external data is generated by
|
||||
```python
|
||||
points = geo.sample_interior(density=20,
|
||||
bounds={x: (0, L)},
|
||||
param_ranges=time_range,
|
||||
low_discrepancy=True)
|
||||
points['u'] = np.sin(points['x']) * (np.sin(c * points['t']) + np.cos(c * points['t']))
|
||||
|
||||
# Some data points are contaminated.
|
||||
points['u'][np.random.choice(len(points['u']), 10, replace=False)] = 3.
|
||||
```
|
||||
|
||||
To use the external data as the data source, we define a data node to store the state:
|
||||
```python
|
||||
@sc.datanode(name='wave_domain', loss_fn='L1')
|
||||
class WaveExternal(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
points = pd.read_csv('external_sample.csv')
|
||||
self.points = {col: points[col].to_numpy().reshape(-1, 1) for col in points.columns}
|
||||
self.constraints = {'u': self.points['u']}
|
||||
self.points.pop('u')
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = self.points
|
||||
constraints = self.constraints
|
||||
return points, constraints
|
||||
|
||||
```
|
||||
If large-scale external data are used, users can also implement the `sampling()` method to adapt to external data interfaces.
|
||||
|
||||
## Define Unknown Parameters
|
||||
|
||||
IDRLnet defines a network node with a single parameter to represent the variable.
|
||||
|
||||
```python
|
||||
var_c = sc.get_net_node(inputs=('x',), outputs=('c',), arch=sc.Arch.single_var)
|
||||
```
|
||||
If bounds for variables are available, users can embed the bounds into the definition.
|
||||
```python
|
||||
var_c = sc.get_net_node(inputs=('x',), outputs=('c',), arch=sc.Arch.bounded_single_var, lower_bound=1., upper_bound=3.0)
|
||||
```
|
||||
## Loss Metrics
|
||||
|
||||
The final loss in each iteration is represented by
|
||||
|
||||
$$
|
||||
loss = \sum_i^M \sigma_i \sum_j^{N_{i}} \lambda_{ij}\times\text{area}_{ij}\times\text{Loss}(y_j, y^{pred}_j),
|
||||
$$
|
||||
where $M$ domains are included, and the $i$-th domain has $N_{i}$ sample points in it.
|
||||
- By default, The loss function is set to `square`, and the alternative is `L1`. More types will be implemented later.
|
||||
- $\text{area}_{ij}$ is the weight generated by geometric objects automatically.
|
||||
- $\sigma_i$ is the weight for the $i$-th domain loss, which is set to `1.` by default.
|
||||
- $\lambda_{ij}$ is the weight for each point.
|
||||
|
||||
For robust regression, the `L1` loss is usually preferred over the `square` loss.
|
||||
The conclusion might also hold for inverse PINN as shown:
|
||||
|
||||
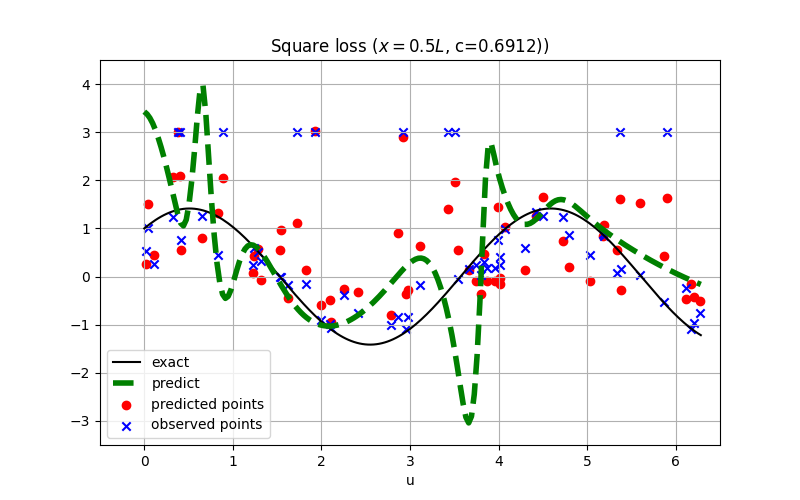
|
||||
|
||||
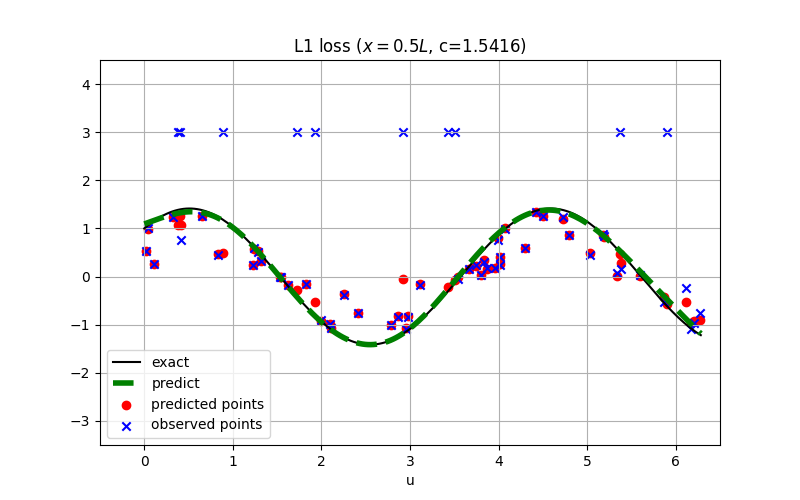
|
||||
|
||||
See `examples/inverse_wave_equation`.
|
||||
|
|
@ -0,0 +1,40 @@
|
|||
# Parameterized Poisson
|
||||
We consider an extended problem of [Simple Poisson](1_simple_poisson.md).
|
||||
|
||||
$$
|
||||
\begin{array}{l}
|
||||
-\Delta u=1\\
|
||||
\frac{\partial u(x, -1)}{\partial n}=\frac{\partial u(x, 1)}{\partial n}=0 \\
|
||||
u(-1,y)=T_l\\
|
||||
u(1, y)=0,
|
||||
\end{array}
|
||||
$$
|
||||
where $T_l$ is a design parameter ranging in $(-0.2,0.2)$.
|
||||
The target is to train a surrogate that $u_\theta(x,y,T_l)$ gives the temperature at $(x,y)$ when $T_l$ is provided.
|
||||
## Train A Surrogate
|
||||
In addition, we define the parameter
|
||||
|
||||
```python
|
||||
temp = sp.Symbol('temp')
|
||||
temp_range = {temp: (-0.2, 0.2)}
|
||||
```
|
||||
|
||||
The usage of `temp` is similar to the time variable in [Burgers' Equation](3_burgers_equation.md).
|
||||
`temp_range` should be passed to the argument `param_ranges` in sampling domains.
|
||||
|
||||
The left bound value condition is
|
||||
```python
|
||||
@sc.datanode
|
||||
class Left(sc.SampleDomain):
|
||||
# Due to `name` is not specified, Left will be the name of datanode automatically
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_boundary(1000, sieve=(sp.Eq(x, -1.)), param_ranges=temp_range)
|
||||
constraints = sc.Variables({'T': temp})
|
||||
return points, constraints
|
||||
```
|
||||
|
||||
The result is shown as follows:
|
||||
|
||||
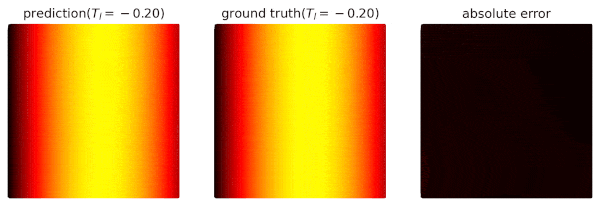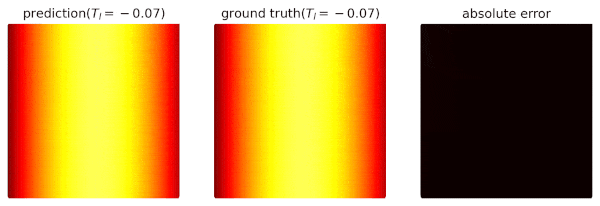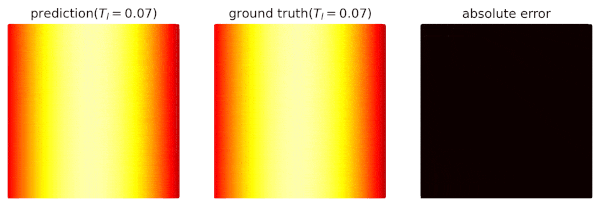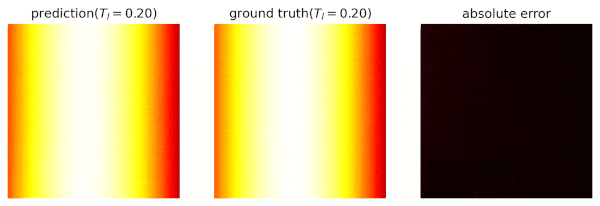
|
||||
|
||||
See `examples/parameterized_poisson`.
|
||||
|
|
@ -0,0 +1,78 @@
|
|||
# Variational Minimization
|
||||
IDRLnet can solve variational minimization problems.
|
||||
In this section, we try to find a minimal surface of revolution.
|
||||
|
||||
Given two points $P_1=(-1, \cosh(-1))$ and $P_2=(0.5, \cosh(0.5))$.
|
||||
Consider a curve $u(x)$ connecting $P_1$ and $P_2$.
|
||||
The surface of revolution is generated by rotating the curve with respect to x-axis.
|
||||
This section aims to find the curve that minimizes the surface area.
|
||||
The surface area of revolution is obtained by integrating over cylinders of radius $y$:
|
||||
|
||||
$$
|
||||
S=\int_{x_1}^{x_2} u(x)\sqrt{u'(x)^2+1}dx.
|
||||
$$
|
||||
|
||||
## Load a Pretrained Network
|
||||
IDRLnet supports loading pretrained networks.
|
||||
For faster convergence, we take the initial network to be the segment connecting $P_1$ and $P_2$,
|
||||
which is accomplished by fitting the following domain:
|
||||
|
||||
```python
|
||||
@sc.datanode(loss_fn='L1')
|
||||
class Interior(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = geo.sample_interior(100)
|
||||
constraints = {'u': (np.cosh(0.5) - np.cosh(-1)) / 1.5 * (x + 1.0) + np.cosh(-1)}
|
||||
return points, constraints
|
||||
```
|
||||
|
||||
The training procedure is derivative-free, so it converges quite fast.
|
||||
|
||||
Starting another script, we load the network trained above as the initial network.
|
||||
|
||||
```python
|
||||
s = sc.Solver(sample_domains=(Boundary(), Interior(), InteriorInfer()),
|
||||
netnodes=[net],
|
||||
init_network_dirs=['pretrain_network_dir'], # where to find the pretrained network
|
||||
pdes=[dx_exp, integral, ],
|
||||
max_iter=1500)
|
||||
```
|
||||
|
||||
## Integral Domain
|
||||
IDRLnet can calculate definite integration on a domain via Monte Carlo methods.
|
||||
|
||||
At the beginning of the script, define `Function` $u$:
|
||||
|
||||
```python
|
||||
u = sp.Function('u')(x)
|
||||
```
|
||||
|
||||
The `ICNode` is responsible for numerical integration.
|
||||
The output of `ICNode` is automatically prefixed with `integral_`.
|
||||
The following code generates a `Node` with output `(integral_dx,)`.
|
||||
|
||||
```python
|
||||
dx_exp = sc.ExpressionNode(expression=sp.Abs(u) * sp.sqrt((u.diff(x)) ** 2 + 1), name='dx')
|
||||
integral = sc.ICNode('dx', dim=1, time=False)
|
||||
```
|
||||
|
||||
Since the minimization model has an obvious lower bound $0$, we embed the problem into the constraints:
|
||||
|
||||
```python
|
||||
@sc.datanode(loss_fn='L1')
|
||||
class Interior(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = geo.sample_interior(10000)
|
||||
constraints = {'integral_dx': 0, }
|
||||
return points, constraints
|
||||
```
|
||||
|
||||
The iterations are show as follows:
|
||||
|
||||

|
||||
|
||||
The exact solution is:
|
||||
|
||||

|
||||
|
||||
See `examples/minimal_surface_of_revolution`.
|
||||
|
|
@ -0,0 +1,42 @@
|
|||
# Volterra Integral Differential Equation
|
||||
We consider the first-order Volterra type integro-differential equation on $[0, 5]$ (from [Lu et al. 2021](https://epubs.siam.org/doi/abs/10.1137/19M1274067)):
|
||||
|
||||
$$
|
||||
\frac{d y}{d x}+y(x)=\int_{0}^{x} e^{t-x} y(t) d t, \quad y(0)=1
|
||||
$$
|
||||
with the ground truth $u=\exp(-x) \cosh x$.
|
||||
|
||||
## 1D integral with Variable Limits
|
||||
The LHS is represented by
|
||||
|
||||
```python
|
||||
exp_lhs = sc.ExpressionNode(expression=f.diff(x) + f, name='lhs')
|
||||
```
|
||||
|
||||
The RHS has an integral with variable limits. Therefore, we introduce the class `Int1DNode`:
|
||||
|
||||
```python
|
||||
fs = sp.Symbol('fs')
|
||||
exp_rhs = sc.Int1DNode(expression=sp.exp(s - x) * fs, var=s, lb=0, ub=x, expression_name='rhs',
|
||||
funs={'fs': {'eval': netnode,
|
||||
'input_map': {'x': 's'},
|
||||
'output_map': {'f': 'fs'}}},
|
||||
degree=10)
|
||||
```
|
||||
We map `f` and `x` to `fs` and `s` in the integral, respectively.
|
||||
The numerical integration is approximated by Gauss–Legendre quadrature with `degree=10`.
|
||||
The difference between the RHS and the LHS is presented by a `pde_op.opterator.Difference` node,
|
||||
|
||||
```python
|
||||
diff = sc.Difference(T='lhs', S='rhs', dim=1, time=False)
|
||||
```
|
||||
|
||||
which generates a node with
|
||||
- `input=(lhs,rhs)`;
|
||||
- `output=(difference_lhs_rhs,)`.
|
||||
|
||||
The final result is shown as follows:
|
||||
|
||||
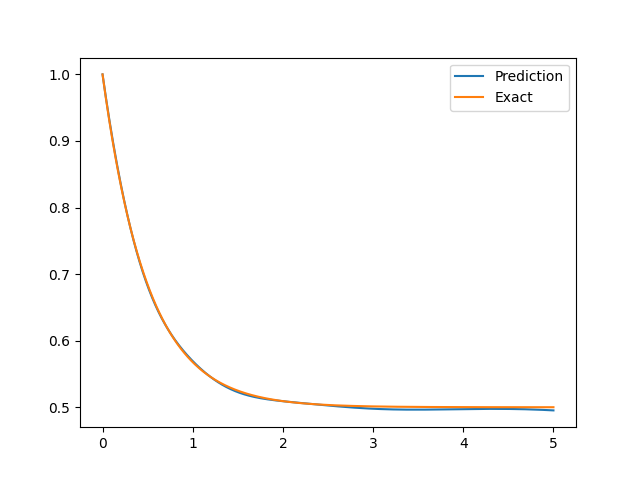
|
||||
|
||||
See `examples/Volterra_IDE`.
|
||||
|
|
@ -0,0 +1,30 @@
|
|||
Tutorial
|
||||
========
|
||||
|
||||
|
||||
To make full use of IDRLnet. We strongly suggest following the following examples:
|
||||
|
||||
1. :ref:`Simple Poisson <Solving Simple Poisson Equation>`. This example introduces the primary usage of IDRLnet. Including creating sampling domains, neural
|
||||
networks, partial differential equations, training, monitoring, and inference.
|
||||
2. :ref:`Euler-Bernoulli beam <Euler–Bernoulli beam>`. The example introduces how to use symbols to construct a PDE node efficiently.
|
||||
3. :ref:`Burgers' Equation <Burgers' Equation>`. The case presents how to include ``time`` in the sampling domains.
|
||||
4. :ref:`Allen-Cahn Equation <Allen-Cahn Equation>`. The example introduces the representation of periodic boundary conditions.
|
||||
``Receiver`` acting as ``callbacks`` are also introduced, including implementing user-defined algorithms and post-processing during the training.
|
||||
5. :ref:`Inverse wave equation <Inverse Wave Equation>`. The example introduces how to discover unknown parameters in PDEs.
|
||||
6. :ref:`Parameterized poisson equation <Parameterized Poisson>`. The example introduces how to train a surrogate with parameters.
|
||||
7. :ref:`Variational Minimization <Variational Minimization>`. The example introduces how to solve variational minimization problems.
|
||||
8. :ref:`Volterra integral differential equation <Volterra Integral Differential Equation>`. The example introduces the way to solve IDEs.
|
||||
|
||||
|
||||
|
||||
.. toctree::
|
||||
:maxdepth: 2
|
||||
|
||||
1_simple_poisson
|
||||
2_euler_beam
|
||||
3_burgers_equation
|
||||
4_allen_cahn
|
||||
5_inverse_wave_equation
|
||||
6_parameterized_poisson
|
||||
7_minimal_surface
|
||||
8_volterra_ide
|
||||
|
|
@ -0,0 +1,14 @@
|
|||
# Installation
|
||||
|
||||
We recommend using conda to manage the environment.
|
||||
Other methods may also work well such like using docker or virtual env.
|
||||
## Anaconda
|
||||
|
||||
```bash
|
||||
git clone https://git.idrl.site/pengwei/idrlnet
|
||||
cd idrlnet
|
||||
conda create -n idrlnet_dev python=3.8 -y
|
||||
conda activate idrlnet_dev
|
||||
pip install -r requirements.txt
|
||||
pip install -e .
|
||||
```
|
||||
|
|
@ -0,0 +1,2 @@
|
|||
# The Team
|
||||
IDRLnet was developed by members of IDRL laboratory.
|
||||
|
|
@ -0,0 +1 @@
|
|||
See [docs for Volterra IDE](../../docs/user/get_started/8_volterra_ide.md).
|
||||
|
|
@ -0,0 +1,61 @@
|
|||
import idrlnet.shortcut as sc
|
||||
import sympy as sp
|
||||
import numpy as np
|
||||
import matplotlib.pyplot as plt
|
||||
|
||||
x = sp.Symbol('x')
|
||||
s = sp.Symbol('s')
|
||||
f = sp.Function('f')(x)
|
||||
geo = sc.Line1D(0, 5)
|
||||
|
||||
|
||||
@sc.datanode
|
||||
def interior():
|
||||
points = geo.sample_interior(1000)
|
||||
constraints = {"difference_lhs_rhs": 0}
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode
|
||||
def init():
|
||||
points = geo.sample_boundary(1, sieve=sp.Eq(x, 0))
|
||||
points['lambda_f'] = 1000 * np.ones_like(points['x'])
|
||||
constraints = {'f': 1}
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode(name='InteriorInfer')
|
||||
def infer():
|
||||
points = {'x': np.linspace(0, 5, 1000).reshape(-1, 1)}
|
||||
return points, {}
|
||||
|
||||
|
||||
netnode = sc.get_net_node(inputs=('x',), outputs=('f',), name='net')
|
||||
exp_lhs = sc.ExpressionNode(expression=f.diff(x) + f, name='lhs')
|
||||
|
||||
fs = sp.Symbol('fs')
|
||||
exp_rhs = sc.Int1DNode(expression=sp.exp(s - x) * fs, var=s, lb=0, ub=x, expression_name='rhs',
|
||||
funs={'fs': {'eval': netnode,
|
||||
'input_map': {'x': 's'},
|
||||
'output_map': {'f': 'fs'}}},
|
||||
degree=10)
|
||||
diff = sc.Difference(T='lhs', S='rhs', dim=1, time=False)
|
||||
|
||||
solver = sc.Solver(sample_domains=(interior(), init(), infer()),
|
||||
netnodes=[netnode],
|
||||
pdes=[exp_lhs, exp_rhs, diff],
|
||||
loading=True,
|
||||
max_iter=3000)
|
||||
solver.solve()
|
||||
points = solver.infer_step({'InteriorInfer': ['x', 'f']})
|
||||
num_x = points['InteriorInfer']['x'].detach().cpu().numpy().ravel()
|
||||
num_f = points['InteriorInfer']['f'].detach().cpu().numpy().ravel()
|
||||
|
||||
fig = plt.figure(figsize=(8,4))
|
||||
plt.plot(num_x, num_f)
|
||||
plt.plot(num_x, np.exp(-num_x) * np.cosh(num_x))
|
||||
plt.xlabel('x')
|
||||
plt.ylabel('y')
|
||||
plt.legend(['Prediction', 'Exact'])
|
||||
plt.savefig('ide.png', dpi=1000, bbox_inches='tight')
|
||||
plt.show()
|
||||
|
|
@ -0,0 +1,158 @@
|
|||
from sympy import Symbol
|
||||
import sympy as sp
|
||||
import numpy as np
|
||||
import matplotlib.pyplot as plt
|
||||
import matplotlib.tri as tri
|
||||
import idrlnet.shortcut as sc
|
||||
import os
|
||||
import torch
|
||||
|
||||
# parameter phase
|
||||
L = 1.
|
||||
|
||||
# define geometry
|
||||
geo = sc.Line1D(-1.0, 1.0)
|
||||
|
||||
# define sympy varaibles to parametize domain curves
|
||||
t_symbol = Symbol('t')
|
||||
x = Symbol('x')
|
||||
u = sp.Function('u')(x, t_symbol)
|
||||
up = sp.Function('up')(x, t_symbol)
|
||||
time_range = {t_symbol: (0, L)}
|
||||
|
||||
|
||||
# constraint phase
|
||||
@sc.datanode
|
||||
class AllenInit(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
return geo.sample_interior(density=300, param_ranges={t_symbol: 0.0}), \
|
||||
{'u': x ** 2 * sp.cos(sp.pi * x), 'lambda_u': 100}
|
||||
|
||||
|
||||
@sc.datanode
|
||||
class AllenBc(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
return geo.sample_boundary(density=200, sieve=sp.Eq(x, -1), param_ranges=time_range), \
|
||||
{'difference_u_up': 0,
|
||||
'difference_diff_u_diff_up': 0,
|
||||
}
|
||||
|
||||
|
||||
@sc.datanode(name='allen_domain')
|
||||
class AllenEq(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
self.points = geo.sample_interior(density=2000, param_ranges=time_range, low_discrepancy=True)
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
constraints = {'AllenCahn_u': 0}
|
||||
return self.points, constraints
|
||||
|
||||
|
||||
@sc.datanode(name='data_evaluate')
|
||||
class AllenPointsInference(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
self.points = geo.sample_interior(density=5000, param_ranges=time_range, low_discrepancy=True)
|
||||
self.points = sc.Variables(self.points).to_torch_tensor_()
|
||||
self.constraints = {'AllenCahn_u': torch.zeros_like(self.points['x'])}
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
return self.points, self.constraints
|
||||
|
||||
|
||||
@sc.datanode(name='re_sampling_domain')
|
||||
class SpaceAdaptiveSampling(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
self.points = geo.sample_interior(density=100, param_ranges=time_range, low_discrepancy=True)
|
||||
self.points = sc.Variables(self.points).to_torch_tensor_()
|
||||
self.constraints = {'AllenCahn_u': torch.zeros_like(self.points['x'])}
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
return self.points, self.constraints
|
||||
|
||||
|
||||
@sc.datanode(name='allen_test')
|
||||
def generate_plot_data():
|
||||
x = np.linspace(-1.0, 1.0, 100)
|
||||
t = np.linspace(0, 1.0, 100)
|
||||
x, t = np.meshgrid(x, t)
|
||||
points = sc.Variables(x=x.reshape(-1, 1), t=t.reshape(-1, 1))
|
||||
return points, {}
|
||||
|
||||
|
||||
# computational node phase
|
||||
|
||||
net_u = sc.MLP([2, 128, 128, 128, 128, 2], activation=sc.Activation.tanh)
|
||||
net_u = sc.NetNode(inputs=('x', 't',), outputs=('u',), name='net1', net=net_u)
|
||||
xp = sc.ExpressionNode(name='xp', expression=x + 2)
|
||||
get_tilde_u = sc.get_shared_net_node(net_u, inputs=('xp', 't',), outputs=('up',), name='net2', arch='mlp')
|
||||
|
||||
diff_u = sc.ExpressionNode(expression=u.diff(x), name='diff_u')
|
||||
diff_up = sc.ExpressionNode(expression=up.diff(x), name='diff_up')
|
||||
|
||||
pde = sc.AllenCahnNode(u='u', gamma_1=0.0001, gamma_2=5)
|
||||
|
||||
boundary_up = sc.Difference(T='diff_u', S='diff_up')
|
||||
boundary_u = sc.Difference(T='u', S='up')
|
||||
|
||||
|
||||
# Receiver hook phase
|
||||
|
||||
class SpaceAdaptiveReceiver(sc.Receiver):
|
||||
def receive_notify(self, solver, message):
|
||||
if sc.Signal.TRAIN_PIPE_END in message.keys() and solver.global_step % 1000 == 0:
|
||||
sc.logger.info('space adaptive sampling...')
|
||||
results = solver.infer_step({'data_evaluate': ['x', 't', 'sdf', 'AllenCahn_u']})
|
||||
residual_data = results['data_evaluate']['AllenCahn_u'].detach().cpu().numpy().ravel()
|
||||
# sort the points by residual loss
|
||||
index = np.argsort(-1. * np.abs(residual_data))[:200]
|
||||
_points = {key: values[index].detach().cpu().numpy() for key, values in results['data_evaluate'].items()}
|
||||
_points.pop('AllenCahn_u')
|
||||
_points['area'] = np.zeros_like(_points['sdf']) + (1.0 / 200)
|
||||
solver.set_domain_parameter('re_sampling_domain', {'points': _points})
|
||||
|
||||
|
||||
class PostProcessReceiver(sc.Receiver):
|
||||
def __init__(self):
|
||||
if not os.path.exists('image'):
|
||||
os.mkdir('image')
|
||||
|
||||
def receive_notify(self, solver, message):
|
||||
if sc.Signal.TRAIN_PIPE_END in message.keys() and solver.global_step % 1000 == 1:
|
||||
sc.logger.info('Post Processing...')
|
||||
points = s.infer_step({'allen_test': ['x', 't', 'u']})
|
||||
triang_total = tri.Triangulation(points['allen_test']['t'].detach().cpu().numpy().ravel(),
|
||||
points['allen_test']['x'].detach().cpu().numpy().ravel(), )
|
||||
plt.tricontourf(triang_total, points['allen_test']['u'].detach().cpu().numpy().ravel(), 100, vmin=-1,
|
||||
vmax=1)
|
||||
tc_bar = plt.colorbar()
|
||||
tc_bar.ax.tick_params(labelsize=12)
|
||||
|
||||
_points = solver.get_domain_parameter('re_sampling_domain', 'points')
|
||||
if not isinstance(_points['t'], torch.Tensor):
|
||||
plt.scatter(_points['t'].ravel(), _points['x'].ravel(), marker='x', s=8)
|
||||
else:
|
||||
plt.scatter(_points['t'].detach().cpu().numpy().ravel(),
|
||||
_points['x'].detach().cpu().numpy().ravel(), marker='x', s=8)
|
||||
|
||||
plt.xlabel('$t$')
|
||||
plt.ylabel('$x$')
|
||||
plt.title('$u(x,t)$')
|
||||
plt.savefig(f'image/result_{solver.global_step}.png')
|
||||
plt.show()
|
||||
|
||||
|
||||
# Solver phase
|
||||
s = sc.Solver(sample_domains=(AllenInit(),
|
||||
AllenBc(),
|
||||
AllenEq(),
|
||||
AllenPointsInference(),
|
||||
SpaceAdaptiveSampling(),
|
||||
generate_plot_data()),
|
||||
netnodes=[net_u, get_tilde_u],
|
||||
pdes=[pde, xp, diff_up, diff_u, boundary_up, boundary_u],
|
||||
max_iter=60000,
|
||||
loading=True)
|
||||
|
||||
s.register_receiver(SpaceAdaptiveReceiver())
|
||||
s.register_receiver(PostProcessReceiver())
|
||||
s.solve()
|
||||
|
|
@ -0,0 +1 @@
|
|||
See [docs for Allen-Cahn](../../docs/user/get_started/4_allen_cahn.md).
|
||||
|
|
@ -0,0 +1,66 @@
|
|||
from sympy import Symbol, sin
|
||||
import math
|
||||
import matplotlib.pyplot as plt
|
||||
import matplotlib.tri as tri
|
||||
import idrlnet.shortcut as sc
|
||||
|
||||
x = Symbol('x')
|
||||
t_symbol = Symbol('t')
|
||||
time_range = {t_symbol: (0, 1)}
|
||||
geo = sc.Line1D(-1., 1.)
|
||||
|
||||
|
||||
@sc.datanode(name='burgers_equation')
|
||||
def interior_domain():
|
||||
points = geo.sample_interior(10000, bounds={x: (-1., 1.)}, param_ranges=time_range)
|
||||
constraints = {'burgers_u': 0}
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode(name='t_boundary')
|
||||
def init_domain():
|
||||
points = geo.sample_interior(100, param_ranges={t_symbol: 0.0})
|
||||
constraints = sc.Variables({'u': -sin(math.pi * x)})
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode(name="x_boundary")
|
||||
def boundary_domain():
|
||||
points = geo.sample_boundary(100, param_ranges=time_range)
|
||||
constraints = sc.Variables({'u': 0})
|
||||
return points, constraints
|
||||
|
||||
|
||||
net = sc.get_net_node(inputs=('x', 't',), outputs=('u',), name='net1', arch=sc.Arch.mlp)
|
||||
pde = sc.BurgersNode(u='u', v=0.01 / math.pi)
|
||||
s = sc.Solver(sample_domains=(interior_domain(), init_domain(), boundary_domain()),
|
||||
netnodes=[net], pdes=[pde], max_iter=4000)
|
||||
s.solve()
|
||||
|
||||
coord = s.infer_step({'burgers_equation': ['x', 't', 'u'], 't_boundary': ['x', 't'],
|
||||
'x_boundary': ['x', 't']})
|
||||
num_x = coord['burgers_equation']['x'].cpu().detach().numpy().ravel()
|
||||
num_t = coord['burgers_equation']['t'].cpu().detach().numpy().ravel()
|
||||
num_u = coord['burgers_equation']['u'].cpu().detach().numpy().ravel()
|
||||
|
||||
init_x = coord['t_boundary']['x'].cpu().detach().numpy().ravel()
|
||||
init_t = coord['t_boundary']['t'].cpu().detach().numpy().ravel()
|
||||
boundary_x = coord['x_boundary']['x'].cpu().detach().numpy().ravel()
|
||||
boundary_t = coord['x_boundary']['t'].cpu().detach().numpy().ravel()
|
||||
|
||||
triang_total = tri.Triangulation(num_t.flatten(), num_x.flatten())
|
||||
u_pre = num_u.flatten()
|
||||
|
||||
fig = plt.figure(figsize=(15, 5))
|
||||
ax1 = fig.add_subplot(221)
|
||||
tcf = ax1.tricontourf(triang_total, u_pre, 100, cmap='jet')
|
||||
tc_bar = plt.colorbar(tcf)
|
||||
tc_bar.ax.tick_params(labelsize=10)
|
||||
ax1.set_xlabel('$t$')
|
||||
ax1.set_ylabel('$x$')
|
||||
ax1.set_title('$u(x,t)$')
|
||||
ax1.scatter(init_t, init_x, c='black', marker='x', s=8)
|
||||
ax1.scatter(boundary_t, boundary_x, c='black', marker='x', s=8)
|
||||
plt.xlim(0, 1)
|
||||
plt.ylim(-1, 1)
|
||||
plt.savefig('Burgers.png', dpi=500, bbox_inches='tight', pad_inches=0.02)
|
||||
|
|
@ -0,0 +1 @@
|
|||
See [docs for Burgers' equations](../../docs/user/get_started/3_burgers_equation.md).
|
||||
|
|
@ -0,0 +1,78 @@
|
|||
import matplotlib.pyplot as plt
|
||||
import sympy as sp
|
||||
import numpy as np
|
||||
import idrlnet.shortcut as sc
|
||||
|
||||
x = sp.symbols('x')
|
||||
Line = sc.Line1D(0, 1)
|
||||
y = sp.Function('y')(x)
|
||||
|
||||
|
||||
@sc.datanode(name='interior')
|
||||
class Interior(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
return Line.sample_interior(1000), {'dddd_y': 0}
|
||||
|
||||
|
||||
@sc.datanode(name='left_boundary1')
|
||||
class LeftBoundary1(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
return Line.sample_boundary(100, sieve=(sp.Eq(x, 0))), {'y': 0}
|
||||
|
||||
|
||||
@sc.datanode(name='left_boundary2')
|
||||
class LeftBoundary2(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
return Line.sample_boundary(100, sieve=(sp.Eq(x, 0))), {'d_y': 0}
|
||||
|
||||
|
||||
@sc.datanode(name='right_boundary1')
|
||||
class RightBoundary1(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
return Line.sample_boundary(100, sieve=(sp.Eq(x, 1))), {'dd_y': 0}
|
||||
|
||||
|
||||
@sc.datanode(name='right_boundary2')
|
||||
class RightBoundary2(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
return Line.sample_boundary(100, sieve=(sp.Eq(x, 1))), {'ddd_y': 0}
|
||||
|
||||
|
||||
@sc.datanode(name='infer')
|
||||
class Infer(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
return {'x': np.linspace(0, 1, 1000).reshape(-1, 1)}, {}
|
||||
|
||||
|
||||
net = sc.get_net_node(inputs=('x',), outputs=('y',), name='net', arch=sc.Arch.mlp)
|
||||
|
||||
pde1 = sc.ExpressionNode(name='dddd_y', expression=y.diff(x).diff(x).diff(x).diff(x) + 1)
|
||||
pde2 = sc.ExpressionNode(name='d_y', expression=y.diff(x))
|
||||
pde3 = sc.ExpressionNode(name='dd_y', expression=y.diff(x).diff(x))
|
||||
pde4 = sc.ExpressionNode(name='ddd_y', expression=y.diff(x).diff(x).diff(x))
|
||||
|
||||
solver = sc.Solver(
|
||||
sample_domains=(Interior(), LeftBoundary1(), LeftBoundary2(), RightBoundary1(), RightBoundary2()),
|
||||
netnodes=[net],
|
||||
pdes=[pde1, pde2, pde3, pde4],
|
||||
max_iter=2000)
|
||||
solver.solve()
|
||||
|
||||
|
||||
# inference
|
||||
def exact(x):
|
||||
return -(x ** 4) / 24 + x ** 3 / 6 - x ** 2 / 4
|
||||
|
||||
|
||||
solver.sample_domains = (Infer(),)
|
||||
points = solver.infer_step({'infer': ['x', 'y']})
|
||||
xs = points['infer']['x'].detach().cpu().numpy().ravel()
|
||||
y_pred = points['infer']['y'].detach().cpu().numpy().ravel()
|
||||
plt.plot(xs, y_pred, label='Pred')
|
||||
y_exact = exact(xs)
|
||||
plt.plot(xs, y_exact, label='Exact', linestyle='--')
|
||||
plt.legend()
|
||||
plt.xlabel('x')
|
||||
plt.ylabel('w')
|
||||
plt.savefig('Euler_beam.png', dpi=300, bbox_inches='tight')
|
||||
plt.show()
|
||||
|
|
@ -0,0 +1 @@
|
|||
See [docs for Euler–Bernoulli beam](../../docs/user/get_started/2_euler_beam.md)
|
||||
|
|
@ -0,0 +1,113 @@
|
|||
import idrlnet.shortcut as sc
|
||||
from math import pi
|
||||
from sympy import Symbol
|
||||
import torch
|
||||
import numpy as np
|
||||
import pandas as pd
|
||||
import os
|
||||
import matplotlib.pyplot as plt
|
||||
|
||||
L = float(pi)
|
||||
|
||||
geo = sc.Line1D(0, L)
|
||||
t_symbol = Symbol('t')
|
||||
x = Symbol('x')
|
||||
time_range = {t_symbol: (0, 2 * L)}
|
||||
c = 1.54
|
||||
external_filename = 'external_sample.csv'
|
||||
|
||||
|
||||
def generate_observed_data():
|
||||
if os.path.exists(external_filename):
|
||||
return
|
||||
points = geo.sample_interior(density=20,
|
||||
bounds={x: (0, L)},
|
||||
param_ranges=time_range,
|
||||
low_discrepancy=True)
|
||||
points['u'] = np.sin(points['x']) * (np.sin(c * points['t']) + np.cos(c * points['t']))
|
||||
points['u'][np.random.choice(len(points['u']), 10, replace=False)] = 3.
|
||||
points = {k: v.ravel() for k, v in points.items()}
|
||||
points = pd.DataFrame.from_dict(points)
|
||||
points.to_csv('external_sample.csv', index=False)
|
||||
|
||||
|
||||
generate_observed_data()
|
||||
|
||||
|
||||
# @sc.datanode(name='wave_domain')
|
||||
@sc.datanode(name='wave_domain', loss_fn='L1')
|
||||
class WaveExternal(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
points = pd.read_csv('external_sample.csv')
|
||||
self.points = {col: points[col].to_numpy().reshape(-1, 1) for col in points.columns}
|
||||
self.constraints = {'u': self.points.pop('u')}
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
return self.points, self.constraints
|
||||
|
||||
|
||||
@sc.datanode(name='wave_external')
|
||||
class WaveEq(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = geo.sample_interior(density=1000, bounds={x: (0, L)}, param_ranges=time_range)
|
||||
constraints = {'wave_equation': 0.}
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode(name='center_infer')
|
||||
class CenterInfer(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
self.points = sc.Variables()
|
||||
self.points['t'] = np.linspace(0, 2 * L, 200).reshape(-1, 1)
|
||||
self.points['x'] = np.ones_like(self.points['t']) * L / 2
|
||||
self.points['area'] = np.ones_like(self.points['t'])
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
return self.points, {}
|
||||
|
||||
|
||||
net = sc.get_net_node(inputs=('x', 't',), outputs=('u',), name='net1', arch=sc.Arch.mlp)
|
||||
var_c = sc.get_net_node(inputs=('x',), outputs=('c',), arch=sc.Arch.single_var)
|
||||
pde = sc.WaveNode(c='c', dim=1, time=True, u='u')
|
||||
s = sc.Solver(sample_domains=(WaveExternal(), WaveEq()),
|
||||
netnodes=[net, var_c],
|
||||
pdes=[pde],
|
||||
# network_dir='square_network_dir',
|
||||
network_dir='network_dir',
|
||||
max_iter=5000)
|
||||
s.solve()
|
||||
|
||||
_, ax = plt.subplots(1, 1, figsize=(8, 4))
|
||||
|
||||
coord = s.infer_step(domain_attr={'wave_domain': ['x', 't', 'u']})
|
||||
num_t = coord['wave_domain']['t'].cpu().detach().numpy().ravel()
|
||||
num_u = coord['wave_domain']['u'].cpu().detach().numpy().ravel()
|
||||
ax.scatter(num_t, num_u, c='r', marker='o', label='predicted points')
|
||||
|
||||
print("true paratmeter c: {:.4f}".format(c))
|
||||
predict_c = var_c.evaluate(torch.Tensor([[1.0]])).item()
|
||||
print("predicted parameter c: {:.4f}".format(predict_c))
|
||||
|
||||
num_t = WaveExternal().sample_fn.points['t'].ravel()
|
||||
num_u = WaveExternal().sample_fn.constraints['u'].ravel()
|
||||
ax.scatter(num_t, num_u, c='b', marker='x', label='observed points')
|
||||
|
||||
s.sample_domains = (CenterInfer(),)
|
||||
points = s.infer_step({'center_infer': ['t', 'x', 'u']})
|
||||
num_t = points['center_infer']['t'].cpu().detach().numpy().ravel()
|
||||
num_u = points['center_infer']['u'].cpu().detach().numpy().ravel()
|
||||
num_x = points['center_infer']['x'].cpu().detach().numpy().ravel()
|
||||
ax.plot(num_t, np.sin(num_x) * (np.sin(c * num_t) + np.cos(c * num_t)), c='k', label='exact')
|
||||
ax.plot(num_t, num_u, '--', c='g', linewidth=4, label='predict')
|
||||
ax.legend()
|
||||
ax.set_xlabel('t')
|
||||
ax.set_ylabel('u')
|
||||
# ax.set_title(f'Square loss ($x=0.5L$, c={predict_c:.4f}))')
|
||||
ax.set_title(f'L1 loss ($x=0.5L$, c={predict_c:.4f})')
|
||||
ax.grid(True)
|
||||
ax.set_xlim([-0.5, 6.5])
|
||||
ax.set_ylim([-3.5, 4.5])
|
||||
# plt.savefig('square.png', dpi=1000, bbox_inches='tight', pad_inches=0.02)
|
||||
plt.savefig('L1.png', dpi=1000, bbox_inches='tight', pad_inches=0.02)
|
||||
plt.show()
|
||||
plt.close()
|
||||
|
|
@ -0,0 +1 @@
|
|||
See [docs for inverse wave equation](../../docs/user/get_started/5_inverse_wave_equation.md)
|
||||
|
|
@ -0,0 +1,143 @@
|
|||
import matplotlib.pyplot as plt
|
||||
from matplotlib import cm
|
||||
import numpy as np
|
||||
import os
|
||||
import sympy as sp
|
||||
from typing import Dict
|
||||
import pickle
|
||||
import math
|
||||
|
||||
import idrlnet.shortcut as sc
|
||||
|
||||
x = sp.Symbol('x')
|
||||
u = sp.Function('u')(x)
|
||||
geo = sc.Line1D(-1, 0.5)
|
||||
|
||||
|
||||
@sc.datanode(sigma=1000.)
|
||||
class Boundary(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
self.points = geo.sample_boundary(1, )
|
||||
self.constraints = {'u': np.cosh(self.points['x'])}
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
return self.points, self.constraints
|
||||
|
||||
|
||||
@sc.datanode(loss_fn='L1')
|
||||
class Interior(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = geo.sample_interior(10000)
|
||||
constraints = {'integral_dx': 0, }
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode
|
||||
class InteriorInfer(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
self.points = sc.Variables()
|
||||
self.points['x'] = np.linspace(-1, 0.5, 1001, endpoint=True).reshape(-1, 1)
|
||||
self.points['area'] = np.ones_like(self.points['x'])
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
return self.points, {}
|
||||
|
||||
|
||||
# plot Intermediate results
|
||||
class PlotReceiver(sc.Receiver):
|
||||
def __init__(self):
|
||||
if not os.path.exists('plot'):
|
||||
os.mkdir('plot')
|
||||
xx = np.linspace(-1, 0.5, 1001, endpoint=True)
|
||||
self.xx = xx
|
||||
angle = np.linspace(0, math.pi * 2, 100)
|
||||
yy = np.cosh(xx)
|
||||
|
||||
xx_mesh, angle_mesh = np.meshgrid(xx, angle)
|
||||
yy_mesh = yy * np.cos(angle_mesh)
|
||||
zz_mesh = yy * np.sin(angle_mesh)
|
||||
|
||||
fig = plt.figure(figsize=(8, 8))
|
||||
ax = fig.gca(projection='3d')
|
||||
ax.set_zlim3d(-1.25 - 1, 0.75 + 1)
|
||||
ax.set_ylim3d(-2, 2)
|
||||
ax.set_xlim3d(-2, 2)
|
||||
|
||||
my_col = cm.cool((yy * np.ones_like(angle_mesh) - 1.0) / 0.6)
|
||||
ax.plot_surface(yy_mesh, zz_mesh, xx_mesh, facecolors=my_col)
|
||||
ax.view_init(elev=15., azim=0)
|
||||
ax.dist = 5
|
||||
plt.axis('off')
|
||||
plt.tight_layout(pad=0., w_pad=0., h_pad=.0)
|
||||
plt.savefig(f'plot/p_exact.png')
|
||||
plt.show()
|
||||
plt.close()
|
||||
self.predict_history = []
|
||||
|
||||
def receive_notify(self, obj: sc.Solver, message: Dict):
|
||||
if sc.Signal.SOLVE_START in message or (sc.Signal.TRAIN_PIPE_END in message and obj.global_step % 200 == 0):
|
||||
print("plotting")
|
||||
points = s.infer_step({'InteriorInfer': ['x', 'u']})
|
||||
num_x = points['InteriorInfer']['x'].detach().cpu().numpy().ravel()
|
||||
num_u = points['InteriorInfer']['u'].detach().cpu().numpy().ravel()
|
||||
angle = np.linspace(0, math.pi * 2, 100)
|
||||
|
||||
xx_mesh, angle_mesh = np.meshgrid(num_x, angle)
|
||||
yy_mesh = num_u * np.cos(angle_mesh)
|
||||
zz_mesh = num_u * np.sin(angle_mesh)
|
||||
|
||||
fig = plt.figure(figsize=(8, 8))
|
||||
ax = fig.gca(projection='3d')
|
||||
ax.set_zlim3d(-1.25 - 1, 0.75 + 1)
|
||||
ax.set_ylim3d(-2, 2)
|
||||
ax.set_xlim3d(-2, 2)
|
||||
|
||||
my_col = cm.cool((num_u * np.ones_like(angle_mesh) - 1.0) / 0.6)
|
||||
ax.plot_surface(yy_mesh, zz_mesh, xx_mesh, facecolors=my_col)
|
||||
ax.view_init(elev=15., azim=0)
|
||||
ax.dist = 5
|
||||
plt.axis('off')
|
||||
plt.tight_layout(pad=0., w_pad=0., h_pad=.0)
|
||||
plt.savefig(f'plot/p_{obj.global_step}.png')
|
||||
plt.show()
|
||||
plt.close()
|
||||
|
||||
self.predict_history.append((num_u, obj.global_step))
|
||||
if sc.Signal.SOLVE_END in message:
|
||||
try:
|
||||
with open('result.pickle', 'rb') as f:
|
||||
self.predict_history = pickle.load(f)
|
||||
except:
|
||||
with open('result.pickle', 'wb') as f:
|
||||
pickle.dump(self.predict_history, f)
|
||||
for yy, step in self.predict_history:
|
||||
if step == 0:
|
||||
plt.plot(yy, self.xx, label=f"iter={step}")
|
||||
if step == 200:
|
||||
plt.plot(yy, self.xx, label=f"iter={step}")
|
||||
if step == 800:
|
||||
plt.plot(yy[::100], self.xx[::100], '-o', label=f"iter={step}")
|
||||
plt.plot(np.cosh(self.xx)[::100], self.xx[::100], '-x', label='exact')
|
||||
plt.plot([0, np.cosh(-1)], [-1, -1], '--', color='gray')
|
||||
plt.plot([0, np.cosh(0.5)], [0.5, 0.5], '--', color='gray')
|
||||
plt.legend()
|
||||
plt.xlim([0, 1.7])
|
||||
plt.xlabel('y')
|
||||
plt.ylabel('x')
|
||||
plt.savefig('iterations.png')
|
||||
plt.show()
|
||||
plt.close()
|
||||
|
||||
|
||||
dx_exp = sc.ExpressionNode(expression=sp.Abs(u) * sp.sqrt((u.diff(x)) ** 2 + 1), name='dx')
|
||||
net = sc.get_net_node(inputs=('x',), outputs=('u',), name='net', arch=sc.Arch.mlp)
|
||||
|
||||
integral = sc.ICNode('dx', dim=1, time=False)
|
||||
|
||||
s = sc.Solver(sample_domains=(Boundary(), Interior(), InteriorInfer()),
|
||||
netnodes=[net],
|
||||
init_network_dirs=['pretrain_network_dir'],
|
||||
pdes=[dx_exp, integral, ],
|
||||
max_iter=1500)
|
||||
s.register_receiver(PlotReceiver())
|
||||
s.solve()
|
||||
|
|
@ -0,0 +1,35 @@
|
|||
import matplotlib.pyplot as plt
|
||||
import numpy as np
|
||||
import sympy as sp
|
||||
import idrlnet.shortcut as sc
|
||||
|
||||
x = sp.Symbol('x')
|
||||
geo = sc.Line1D(-1, 0.5)
|
||||
|
||||
|
||||
@sc.datanode(loss_fn='L1')
|
||||
class Interior(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = geo.sample_interior(100)
|
||||
constraints = {'u': (np.cosh(0.5) - np.cosh(-1)) / 1.5 * (x + 1.0) + np.cosh(-1)}
|
||||
return points, constraints
|
||||
|
||||
|
||||
net = sc.get_net_node(inputs=('x',), outputs=('u',), name='net', arch=sc.Arch.mlp)
|
||||
|
||||
s = sc.Solver(sample_domains=(Interior(),),
|
||||
netnodes=[net],
|
||||
pdes=[],
|
||||
network_dir='pretrain_network_dir',
|
||||
max_iter=1000)
|
||||
s.solve()
|
||||
|
||||
points = s.infer_step({'Interior': ['x', 'u']})
|
||||
num_x = points['Interior']['x'].detach().cpu().numpy().ravel()
|
||||
num_u = points['Interior']['u'].detach().cpu().numpy().ravel()
|
||||
|
||||
xx = np.linspace(-1, 0.5, 1000, endpoint=True)
|
||||
yy = np.cosh(xx)
|
||||
plt.plot(xx, yy)
|
||||
plt.plot(num_x, num_u)
|
||||
plt.show()
|
||||
|
|
@ -0,0 +1,5 @@
|
|||
1. run `python minimal_surface_of_revolution_pretrain.py`
|
||||
2. run `python minimal_surface_of_revolution.py`
|
||||
|
||||
See [docs for minimal surface](../../docs/user/get_started/7_minimal_surface.md)
|
||||
|
||||
|
|
@ -0,0 +1,92 @@
|
|||
import idrlnet.shortcut as sc
|
||||
import sympy as sp
|
||||
import matplotlib.pyplot as plt
|
||||
import matplotlib.tri as tri
|
||||
import numpy as np
|
||||
|
||||
x, y = sp.symbols('x y')
|
||||
temp = sp.Symbol('temp')
|
||||
temp_range = {temp: (-0.2, 0.2)}
|
||||
rec = sc.Rectangle((-1., -1.), (1., 1.))
|
||||
|
||||
|
||||
@sc.datanode
|
||||
class Right(sc.SampleDomain):
|
||||
# Due to `name` is not specified, Right will be the name of datanode automatically
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_boundary(1000, sieve=(sp.Eq(x, 1.)), param_ranges=temp_range)
|
||||
constraints = sc.Variables({'T': 0.})
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode
|
||||
class Left(sc.SampleDomain):
|
||||
# Due to `name` is not specified, Left will be the name of datanode automatically
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_boundary(1000, sieve=(sp.Eq(x, -1.)), param_ranges=temp_range)
|
||||
constraints = sc.Variables({'T': temp})
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode(name="up_down")
|
||||
class UpDownBoundaryDomain(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_boundary(1000, sieve=((x > -1.) & (x < 1.)), param_ranges=temp_range)
|
||||
constraints = sc.Variables({'normal_gradient_T': 0.})
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode(name="heat_domain")
|
||||
class HeatDomain(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
self.points = 1000
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_interior(self.points, param_ranges=temp_range)
|
||||
constraints = sc.Variables({'diffusion_T': 1.})
|
||||
return points, constraints
|
||||
|
||||
|
||||
net = sc.get_net_node(inputs=('x', 'y', 'temp'), outputs=('T',), name='net1', arch=sc.Arch.mlp)
|
||||
pde = sc.DiffusionNode(T='T', D=1., Q=0., dim=2, time=False)
|
||||
grad = sc.NormalGradient('T', dim=2, time=False)
|
||||
s = sc.Solver(sample_domains=(HeatDomain(), Left(), Right(), UpDownBoundaryDomain()),
|
||||
netnodes=[net],
|
||||
pdes=[pde, grad],
|
||||
max_iter=3000)
|
||||
s.solve()
|
||||
|
||||
|
||||
def infer_temp(temp_num, file_suffix=None):
|
||||
temp_range[temp] = temp_num
|
||||
s.set_domain_parameter('heat_domain', {'points': 10000})
|
||||
coord = s.infer_step({'heat_domain': ['x', 'y', 'T']})
|
||||
num_x = coord['heat_domain']['x'].cpu().detach().numpy().ravel()
|
||||
num_y = coord['heat_domain']['y'].cpu().detach().numpy().ravel()
|
||||
num_Tp = coord['heat_domain']['T'].cpu().detach().numpy().ravel()
|
||||
|
||||
# Ground truth
|
||||
num_T = -(num_x + 1 + temp_num) * (num_x - 1.) / 2
|
||||
|
||||
fig, ax = plt.subplots(1, 3, figsize=(10, 3))
|
||||
triang_total = tri.Triangulation(num_x, num_y)
|
||||
ax[0].tricontourf(triang_total, num_Tp, 100, cmap='hot', vmin=-0.2, vmax=1.21 / 2)
|
||||
ax[0].axis('off')
|
||||
ax[0].set_title(f'prediction($T_l={temp_num:.2f}$)')
|
||||
ax[1].tricontourf(triang_total, num_T, 100, cmap='hot', vmin=-0.2, vmax=1.21 / 2)
|
||||
ax[1].axis('off')
|
||||
ax[1].set_title(f'ground truth($T_l={temp_num:.2f}$)')
|
||||
ax[2].tricontourf(triang_total, np.abs(num_T - num_Tp), 100, cmap='hot', vmin=0, vmax=1.21 / 2)
|
||||
ax[2].axis('off')
|
||||
ax[2].set_title('absolute error')
|
||||
if file_suffix is None:
|
||||
plt.savefig(f'poisson_{temp_num:.2f}.png', dpi=300, bbox_inches='tight')
|
||||
plt.show()
|
||||
else:
|
||||
plt.savefig(f'poisson_{file_suffix}.png', dpi=300, bbox_inches='tight')
|
||||
plt.show()
|
||||
|
||||
|
||||
for i in range(41):
|
||||
temp_num = i / 100 - 0.2
|
||||
infer_temp(temp_num, file_suffix=i)
|
||||
|
|
@ -0,0 +1 @@
|
|||
See [docs for Parameterized Poisson](../../docs/user/get_started/6_parameterized_poisson.md).
|
||||
|
|
@ -0,0 +1 @@
|
|||
See [docs for Simple Poisson](../../docs/user/get_started/1_simple_poisson.md).
|
||||
|
|
@ -0,0 +1,70 @@
|
|||
import idrlnet.shortcut as sc
|
||||
import sympy as sp
|
||||
import matplotlib.pyplot as plt
|
||||
import matplotlib.tri as tri
|
||||
import numpy as np
|
||||
|
||||
x, y = sp.symbols('x y')
|
||||
rec = sc.Rectangle((-1., -1.), (1., 1.))
|
||||
|
||||
|
||||
@sc.datanode
|
||||
class LeftRight(sc.SampleDomain):
|
||||
# Due to `name` is not specified, LeftRight will be the name of datanode automatically
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_boundary(1000, sieve=((y > -1.) & (y < 1.)))
|
||||
constraints = {'T': 0.}
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode(name="up_down")
|
||||
class UpDownBoundaryDomain(sc.SampleDomain):
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_boundary(1000, sieve=((x > -1.) & (x < 1.)))
|
||||
constraints = {'normal_gradient_T': 0.}
|
||||
return points, constraints
|
||||
|
||||
|
||||
@sc.datanode(name="heat_domain")
|
||||
class HeatDomain(sc.SampleDomain):
|
||||
def __init__(self):
|
||||
self.points = 1000
|
||||
|
||||
def sampling(self, *args, **kwargs):
|
||||
points = rec.sample_interior(self.points)
|
||||
constraints = {'diffusion_T': 1.}
|
||||
return points, constraints
|
||||
|
||||
|
||||
net = sc.get_net_node(inputs=('x', 'y',), outputs=('T',), name='net1', arch=sc.Arch.mlp)
|
||||
pde = sc.DiffusionNode(T='T', D=1., Q=0., dim=2, time=False)
|
||||
grad = sc.NormalGradient('T', dim=2, time=False)
|
||||
s = sc.Solver(sample_domains=(HeatDomain(), LeftRight(), UpDownBoundaryDomain()),
|
||||
netnodes=[net],
|
||||
pdes=[pde, grad],
|
||||
max_iter=1000)
|
||||
s.solve()
|
||||
|
||||
# Inference
|
||||
s.set_domain_parameter('heat_domain', {'points': 10000})
|
||||
coord = s.infer_step({'heat_domain': ['x', 'y', 'T']})
|
||||
num_x = coord['heat_domain']['x'].cpu().detach().numpy().ravel()
|
||||
num_y = coord['heat_domain']['y'].cpu().detach().numpy().ravel()
|
||||
num_Tp = coord['heat_domain']['T'].cpu().detach().numpy().ravel()
|
||||
|
||||
# Ground truth
|
||||
num_T = -num_x * num_x / 2 + 0.5
|
||||
|
||||
fig, ax = plt.subplots(1, 3, figsize=(10, 3))
|
||||
triang_total = tri.Triangulation(num_x, num_y)
|
||||
ax[0].tricontourf(triang_total, num_Tp, 100, cmap='hot', vmin=0, vmax=0.5)
|
||||
ax[0].axis('off')
|
||||
ax[0].set_title('prediction')
|
||||
ax[1].tricontourf(triang_total, num_T, 100, cmap='hot', vmin=0, vmax=0.5)
|
||||
ax[1].axis('off')
|
||||
ax[1].set_title('ground truth')
|
||||
ax[2].tricontourf(triang_total, np.abs(num_T - num_Tp), 100, cmap='hot', vmin=0, vmax=0.5)
|
||||
ax[2].axis('off')
|
||||
ax[2].set_title('absolute error')
|
||||
|
||||
plt.savefig('simple_poisson.png', dpi=300, bbox_inches='tight')
|
||||
|
|
@ -0,0 +1,15 @@
|
|||
import torch
|
||||
# todo more careful check
|
||||
GPU_ENABLED = True
|
||||
if torch.cuda.is_available():
|
||||
try:
|
||||
_ = torch.Tensor([0., 0.]).cuda()
|
||||
torch.set_default_tensor_type('torch.cuda.FloatTensor')
|
||||
print('gpu available')
|
||||
GPU_ENABLED = True
|
||||
except:
|
||||
print('gpu not available')
|
||||
GPU_ENABLED = False
|
||||
else:
|
||||
print('gpu not available')
|
||||
GPU_ENABLED = False
|
||||
|
|
@ -0,0 +1,2 @@
|
|||
from .layer import *
|
||||
from .mlp import *
|
||||
|
|
@ -0,0 +1,151 @@
|
|||
""" The module is experimental. It may be removed or totally refactored in the future."""
|
||||
|
||||
import idrlnet.architecture.mlp as mlp
|
||||
import itertools
|
||||
import torch
|
||||
from typing import List, Tuple, Union, Dict
|
||||
from idrlnet.geo_utils.geo_obj import Rectangle
|
||||
from idrlnet.net import NetNode
|
||||
from idrlnet.pde_op.operator import Difference
|
||||
from idrlnet.data import get_data_node
|
||||
|
||||
|
||||
def indicator(xn: torch.Tensor, *axis_bounds):
|
||||
# todo: use `heavyside`
|
||||
i = 0
|
||||
lb, ub, lb_eq = axis_bounds[0]
|
||||
if lb_eq:
|
||||
indic = torch.logical_and(xn[:, i:i + 1] >= axis_bounds[0][0], axis_bounds[0][1] >= xn[:, i:i + 1])
|
||||
else:
|
||||
indic = torch.logical_and(xn[:, i:i + 1] > axis_bounds[0][0], axis_bounds[0][1] >= xn[:, i:i + 1])
|
||||
for i, (lb, ub, lb_eq) in enumerate(axis_bounds[1:]):
|
||||
if lb_eq:
|
||||
indic = torch.logical_and(indic, torch.logical_and(xn[:, i + 1:i + 2] >= lb, ub >= xn[:, i + 1:i + 2]))
|
||||
else:
|
||||
indic = torch.logical_and(indic, torch.logical_and(xn[:, i + 1:i + 2] > lb, ub >= xn[:, i + 1:i + 2]))
|
||||
return indic
|
||||
|
||||
|
||||
class NetEval(torch.nn.Module):
|
||||
def __init__(self, n_inputs: int, n_outputs: int, columns, rows, **kwargs):
|
||||
super().__init__()
|
||||
self.columns = columns
|
||||
self.rows = rows
|
||||
self.n_columns = len(self.columns) - 1
|
||||
self.n_rows = len(self.rows) - 1
|
||||
self.nets = []
|
||||
if 'net_generator' in kwargs.keys():
|
||||
net_gen = kwargs.pop('net_generator')
|
||||
else:
|
||||
net_gen = lambda: mlp.MLP([n_inputs, 20, 20, 20, 20, n_outputs])
|
||||
for i in range(self.n_columns):
|
||||
self.nets.append([])
|
||||
for i in range(self.n_columns):
|
||||
for j in range(self.n_rows):
|
||||
self.nets[i].append(net_gen())
|
||||
self.layers = torch.nn.ModuleList(itertools.chain(*self.nets))
|
||||
|
||||
def forward(self, x):
|
||||
xn = x.detach()
|
||||
y = 0
|
||||
for i in range(self.n_columns):
|
||||
for j in range(self.n_rows):
|
||||
y += indicator(xn, (self.columns[i], self.columns[i + 1], True if i == 0 else False),
|
||||
(self.rows[j], self.rows[j + 1], True if j == 0 else False)) * self.nets[i][j](x)
|
||||
return y
|
||||
|
||||
|
||||
class Interface:
|
||||
def __init__(self, points1, points2, nr, outputs, i1, j1, i2, j2, overlap=0.2):
|
||||
x_min, x_max = min(points1[0], points2[0]), max(points1[0], points2[0])
|
||||
y_min, y_max = min(points1[1], points2[1]), max(points1[1], points2[1])
|
||||
self.geo = Rectangle((x_min - overlap / 2, y_min - overlap / 2), (x_max + overlap / 2, y_max + overlap / 2))
|
||||
self.nr = nr
|
||||
self.outputs = outputs
|
||||
self.i1 = i1
|
||||
self.j1 = j1
|
||||
self.i2 = i2
|
||||
self.j2 = j2
|
||||
|
||||
def __call__(self, *args, **kwargs):
|
||||
points = self.geo.sample_boundary(self.nr)
|
||||
return points, {f'difference_{output}_{self.i1}_{self.j1}_{output}_{self.i2}_{self.j2}': 0
|
||||
for output in self.outputs}
|
||||
|
||||
|
||||
class NetGridNode(NetNode):
|
||||
def __init__(self, inputs: Union[Tuple, List[str]], outputs: Union[Tuple, List[str]],
|
||||
x_segments: List[float] = None, y_segments: List[float] = None,
|
||||
z_segments: List[float] = None, t_segments: List[float] = None, columns: List[float] = None,
|
||||
rows: List[float] = None, *args,
|
||||
**kwargs):
|
||||
if columns is None:
|
||||
columns = []
|
||||
if rows is None:
|
||||
rows = []
|
||||
require_no_grad = False
|
||||
fixed = False
|
||||
self.columns = columns
|
||||
self.rows = rows
|
||||
self.main_net = NetEval(n_inputs=len(inputs), n_outputs=len(outputs), columns=columns, rows=rows, **kwargs)
|
||||
super(NetGridNode, self).__init__(inputs, outputs, self.main_net, fixed, require_no_grad, *args, **kwargs)
|
||||
|
||||
def get_grid(self, overlap, nr_points_per_interface_area=100):
|
||||
n_columns = self.main_net.n_columns
|
||||
n_rows = self.main_net.n_rows
|
||||
netnodes = []
|
||||
eqs = []
|
||||
constraints = []
|
||||
for i in range(n_columns):
|
||||
for j in range(n_rows):
|
||||
nn = NetNode(inputs=self.inputs,
|
||||
outputs=tuple(f'{output}_{i}_{j}' for output in self.outputs),
|
||||
net=self.main_net.nets[i][j],
|
||||
name=f'{self.name}[{i}][{j}]')
|
||||
nn.is_reference = True
|
||||
netnodes.append(nn)
|
||||
if i > 0:
|
||||
for output in self.outputs:
|
||||
diff_Node = Difference(f'{output}_{i - 1}_{j}', f'{output}_{i}_{j}', dim=2, time=False)
|
||||
eqs.append(diff_Node)
|
||||
|
||||
interface = Interface((self.columns[i], self.rows[j]), (self.columns[i], self.rows[j + 1]),
|
||||
nr_points_per_interface_area, self.outputs, i - 1, j, i, j, overlap=overlap)
|
||||
|
||||
constraints.append(get_data_node(interface, name=f'interface[{i - 1}][{j}]_[{i}][{j}]'))
|
||||
if j > 0:
|
||||
for output in self.outputs:
|
||||
diff_Node = Difference(f'{output}_{i}_{j - 1}', f'{output}_{i}_{j}', dim=2, time=False)
|
||||
eqs.append(diff_Node)
|
||||
|
||||
interface = Interface((self.columns[i], self.rows[j]), (self.columns[i + 1], self.rows[j]),
|
||||
nr_points_per_interface_area, self.outputs, i, j - 1, i, j, overlap=overlap)
|
||||
|
||||
constraints.append(get_data_node(interface, name=f'interface[{i}][{j - 1}]_[{i}][{j}]'))
|
||||
return netnodes, eqs, constraints
|
||||
|
||||
|
||||
def get_net_reg_grid_2d(inputs: Union[Tuple, List[str]], outputs: Union[Tuple, List[str]], name: str,
|
||||
columns: List[float], rows: List[float], **kwargs):
|
||||
if 'overlap' in kwargs.keys():
|
||||
overlap = kwargs.pop('overlap')
|
||||
else:
|
||||
overlap = 0.2
|
||||
net = NetGridNode(inputs=inputs, outputs=outputs, columns=columns, rows=rows, name=name, **kwargs)
|
||||
nets, eqs, interfaces = net.get_grid(nr_points_per_interface_area=1000, overlap=overlap)
|
||||
nets.append(net)
|
||||
return nets, eqs, interfaces
|
||||
|
||||
|
||||
def get_net_reg_grid(inputs: Union[Tuple, List[str]], outputs: Union[Tuple, List[str]], name: str,
|
||||
x_segments: List[float] = None, y_segments: List[float] = None, z_segments: List[float] = None,
|
||||
t_segments: List[float] = None, **kwargs):
|
||||
if 'overlap' in kwargs.keys():
|
||||
overlap = kwargs.pop('overlap')
|
||||
else:
|
||||
overlap = 0.2
|
||||
net = NetGridNode(inputs=inputs, outputs=outputs, x_segments=x_segments, y_segments=y_segments,
|
||||
z_segments=z_segments, t_segments=t_segments, name=name, **kwargs)
|
||||
nets, eqs, interfaces = net.get_grid(nr_points_per_interface_area=1000, overlap=overlap)
|
||||
nets.append(net)
|
||||
return nets, eqs, interfaces
|
||||
|
|
@ -0,0 +1,149 @@
|
|||
""" The module provide elements for construct MLP."""
|
||||
|
||||
import enum
|
||||
import math
|
||||
import torch
|
||||
from idrlnet.header import logger
|
||||
|
||||
__all__ = ['Activation', 'Initializer', 'get_activation_layer', 'get_linear_layer']
|
||||
|
||||
|
||||
class Activation(enum.Enum):
|
||||
relu = 'relu'
|
||||
silu = 'silu'
|
||||
selu = 'selu'
|
||||
sigmoid = 'sigmoid'
|
||||
tanh = 'tanh'
|
||||
swish = 'swish'
|
||||
poly = 'poly'
|
||||
sin = 'sin'
|
||||
leaky_relu = 'leaky_relu'
|
||||
|
||||
|
||||
class Initializer(enum.Enum):
|
||||
Xavier_uniform = 'Xavier_uniform'
|
||||
constant = 'constant'
|
||||
kaiming_uniform = 'kaiming_uniform'
|
||||
default = 'default'
|
||||
|
||||
|
||||
def get_linear_layer(input_dim: int, output_dim: int, weight_norm=False,
|
||||
initializer: Initializer = Initializer.Xavier_uniform, *args,
|
||||
**kwargs):
|
||||
layer = torch.nn.Linear(input_dim, output_dim)
|
||||
init_method = InitializerFactory.get_initializer(initializer=initializer, **kwargs)
|
||||
init_method(layer.weight)
|
||||
torch.nn.init.constant_(layer.bias, 0.)
|
||||
if weight_norm:
|
||||
layer = torch.nn.utils.weight_norm(layer)
|
||||
return layer
|
||||
|
||||
|
||||
def get_activation_layer(activation: Activation = Activation.swish, *args, **kwargs):
|
||||
return ActivationFactory.get_from_string(activation)
|
||||
|
||||
|
||||
def modularize(fun_generator):
|
||||
def wrapper(fun):
|
||||
class _LambdaModule(torch.nn.Module):
|
||||
def __init__(self):
|
||||
super().__init__()
|
||||
self.fun = fun_generator(fun)
|
||||
|
||||
def forward(self, x):
|
||||
# x = self.fun(-x)
|
||||
x = self.fun(x)
|
||||
return x
|
||||
|
||||
return type(fun.name, (_LambdaModule,), {})()
|
||||
|
||||
return wrapper
|
||||
|
||||
|
||||
class ActivationFactory:
|
||||
@staticmethod
|
||||
@modularize
|
||||
def get_from_string(activation: Activation, *args, **kwargs):
|
||||
if activation == Activation.relu:
|
||||
return torch.relu
|
||||
elif activation == Activation.selu:
|
||||
return torch.selu
|
||||
elif activation == Activation.sigmoid:
|
||||
return torch.sigmoid
|
||||
elif activation == Activation.tanh:
|
||||
return torch.tanh
|
||||
elif activation == Activation.swish:
|
||||
return swish
|
||||
elif activation == Activation.poly:
|
||||
return poly
|
||||
elif activation == Activation.sin:
|
||||
return torch.sin
|
||||
elif activation == Activation.silu:
|
||||
return Silu()
|
||||
else:
|
||||
logger.error(f'Activation {activation} is not supported!')
|
||||
raise NotImplementedError('Activation ' + activation.name + ' is not supported')
|
||||
|
||||
|
||||
class Silu:
|
||||
def __init__(self):
|
||||
try:
|
||||
self.m = torch.nn.SiLU()
|
||||
except:
|
||||
self.m = lambda x: x * torch.sigmoid(x)
|
||||
|
||||
def __call__(self, x):
|
||||
return self.m(x)
|
||||
|
||||
|
||||
def leaky_relu(x, leak=0.1):
|
||||
f1 = 0.5 * (1 + leak)
|
||||
f2 = 0.5 * (1 - leak)
|
||||
return f1 * x + f2 * abs(x)
|
||||
|
||||
|
||||
def triangle_wave(x):
|
||||
y = 0.0
|
||||
for i in range(3):
|
||||
y += (-1.0) ** (i) * torch.sin(2.0 * math.pi * (2.0 * i + 1.0) * x) / (2.0 * i + 1.0) ** (2)
|
||||
y = 0.5 * (8 / (math.pi ** 2) * y) + .5
|
||||
return y
|
||||
|
||||
|
||||
def swish(x):
|
||||
return x * torch.sigmoid(x)
|
||||
|
||||
|
||||
def hard_swish(x):
|
||||
return x * torch.sigmoid(100.0 * x)
|
||||
|
||||
|
||||
def poly(x):
|
||||
axis = len(x.get_shape()) - 1
|
||||
return torch.cat([x ** 3, x ** 2, x], axis)
|
||||
|
||||
|
||||
def fourier(x, terms=10):
|
||||
axis = len(x.get_shape()) - 1
|
||||
x_list = []
|
||||
for i in range(terms):
|
||||
x_list.append(torch.sin(2 * math.pi * i * x))
|
||||
x_list.append(torch.cos(2 * math.pi * i * x))
|
||||
return torch.cat(x_list, axis)
|
||||
|
||||
|
||||
class InitializerFactory:
|
||||
@staticmethod
|
||||
def get_initializer(initializer: Initializer, *args, **kwargs):
|
||||
# todo: more
|
||||
if initializer == Initializer.Xavier_uniform:
|
||||
return torch.nn.init.xavier_uniform_
|
||||
elif initializer == Initializer.constant:
|
||||
return lambda x: torch.nn.init.constant_(x, kwargs['constant'])
|
||||
elif initializer == Initializer.kaiming_uniform:
|
||||
return lambda x: torch.nn.init.kaiming_uniform_(x, mode='fan_in', nonlinearity='relu')
|
||||
elif initializer == Initializer.default:
|
||||
return lambda x: x
|
||||
else:
|
||||
logger.error('initialization ' + initializer.name + ' is not supported')
|
||||
raise NotImplementedError('initialization ' + initializer.name + ' is not supported')
|
||||
|
|
@ -0,0 +1,242 @@
|
|||
"""This module provide some MLP architectures."""
|
||||
|
||||
import torch
|
||||
import math
|
||||
from collections import OrderedDict
|
||||
from idrlnet.architecture.layer import get_linear_layer, get_activation_layer, Initializer, Activation
|
||||
from typing import List, Union, Tuple
|
||||
from idrlnet.header import logger
|
||||
from idrlnet.net import NetNode
|
||||
import enum
|
||||
|
||||
|
||||
class MLP(torch.nn.Module):
|
||||
"""A subclass of torch.nn.Module customizes a multiple linear perceptron network.
|
||||
|
||||
:param n_seq: Define neuron numbers in each layer. The number of the first and the last should be in
|
||||
keeping with inputs and outputs.
|
||||
:type n_seq: List[int]
|
||||
:param activation: By default, the activation is `Activation.swish`.
|
||||
:type activation: Union[Activation,List[Activation]]
|
||||
:param initialization:
|
||||
:type initialization:Initializer
|
||||
:param weight_norm: If weight normalization is used.
|
||||
:type weight_norm: bool
|
||||
:param name: Symbols will appear in the name of each layer. Do not confuse with the netnode name.
|
||||
:type name: str
|
||||
:param args:
|
||||
:param kwargs:
|
||||
"""
|
||||
|
||||
def __init__(self, n_seq: List[int], activation: Union[Activation, List[Activation]] = Activation.swish,
|
||||
initialization: Initializer = Initializer.kaiming_uniform,
|
||||
weight_norm: bool = True, name: str = 'mlp', *args, **kwargs):
|
||||
super().__init__()
|
||||
self.layers = OrderedDict()
|
||||
current_activation = ''
|
||||
assert isinstance(n_seq, Activation) or isinstance(n_seq, list)
|
||||
for i in range(len(n_seq) - 1):
|
||||
if isinstance(activation, list):
|
||||
current_activation = activation[i]
|
||||
elif i < len(n_seq) - 2:
|
||||
current_activation = activation
|
||||
self.layers['{}_{}'.format(name, i)] = get_linear_layer(n_seq[i], n_seq[i + 1], weight_norm, initialization,
|
||||
*args, **kwargs)
|
||||
if (isinstance(activation, Activation) and i < len(n_seq) - 2) or isinstance(activation, list):
|
||||
if current_activation == 'none':
|
||||
continue
|
||||
self.layers['{}_{}_activation'.format(name, i)] = get_activation_layer(current_activation, *args,
|
||||
**kwargs)
|
||||
self.layers = torch.nn.ModuleDict(self.layers)
|
||||
|
||||
def forward(self, x):
|
||||
n_layers = len(self.layers)
|
||||
i = 0
|
||||
for name, layer in self.layers.items():
|
||||
x = layer(x)
|
||||
if i == n_layers - 1:
|
||||
break
|
||||
i += 1
|
||||
return x
|
||||
|
||||
|
||||
class Siren(torch.nn.Module):
|
||||
def __init__(self, n_seq: List[int], first_omega: float = 30.0,
|
||||
omega: float = 30.0, name: str = 'siren', *args, **kwargs):
|
||||
super().__init__()
|
||||
self.layers = OrderedDict()
|
||||
self.first_omega = first_omega
|
||||
self.omega = omega
|
||||
assert isinstance(n_seq, str) or isinstance(n_seq, list)
|
||||
for i in range(len(n_seq) - 1):
|
||||
if i == 0:
|
||||
self.layers['{}_{}'.format(name, i)] = self.get_siren_layer(n_seq[i], n_seq[i + 1], True, first_omega)
|
||||
else:
|
||||
self.layers['{}_{}'.format(name, i)] = self.get_siren_layer(n_seq[i], n_seq[i + 1], False, omega)
|
||||
if i < (len(n_seq) - 2):
|
||||
self.layers['{}_{}_activation'.format(name, i)] = get_activation_layer(Activation.sin, *args, **kwargs)
|
||||
|
||||
self.layers = torch.nn.ModuleDict(self.layers)
|
||||
|
||||
@staticmethod
|
||||
def get_siren_layer(input_dim: int, output_dim: int, is_first: bool, omega_0: float):
|
||||
layer = torch.nn.Linear(input_dim, output_dim)
|
||||
dim = input_dim
|
||||
if is_first:
|
||||
torch.nn.init.uniform_(layer.weight.data, -1.0 / dim, 1.0 / dim)
|
||||
else:
|
||||
torch.nn.init.uniform_(layer.weight.data, -1.0 * math.sqrt(6.0 / dim) / omega_0,
|
||||
math.sqrt(6.0 / dim) / omega_0)
|
||||
torch.nn.init.uniform_(layer.bias.data, -1 * math.sqrt(1 / dim), math.sqrt(1 / dim))
|
||||
return layer
|
||||
|
||||
def forward(self, x):
|
||||
i = 0
|
||||
n_layers = len(self.layers)
|
||||
for name, layer in self.layers.items():
|
||||
x = layer(x)
|
||||
if isinstance(layer, torch.nn.Linear) and i < n_layers - 1:
|
||||
x = self.first_omega * x if i == 0 else self.omega * x
|
||||
i += 1
|
||||
return x
|
||||
|
||||
|
||||
class SingleVar(torch.nn.Module):
|
||||
"""Wrapper a single parameter to represent an unknown coefficient in inverse problem.
|
||||
|
||||
:param initialization: initialization value for the parameter. The default is 0.01
|
||||
:type initialization: float
|
||||
"""
|
||||
|
||||
def __init__(self, initialization: float = 1.0):
|
||||
super().__init__()
|
||||
self.value = torch.nn.Parameter(torch.Tensor([initialization]))
|
||||
|
||||
def forward(self, x) -> torch.Tensor:
|
||||
return x[:, :1] * 0. + self.value
|
||||
|
||||
def get_value(self) -> torch.Tensor:
|
||||
return self.value
|
||||
|
||||
|
||||
class BoundedSingleVar(torch.nn.Module):
|
||||
"""Wrapper a single parameter to represent an unknown coefficient in inverse problem with the upper and lower bound.
|
||||
|
||||
:param lower_bound: The lower bound for the parameter.
|
||||
:type lower_bound: float
|
||||
:param upper_bound: The upper bound for the parameter.
|
||||
:type upper_bound: float
|
||||
"""
|
||||
|
||||
def __init__(self, lower_bound, upper_bound):
|
||||
super().__init__()
|
||||
self.value = torch.nn.Parameter(torch.Tensor([0.0]))
|
||||
self.layer = torch.nn.Sigmoid()
|
||||
self.ub, self.lb = upper_bound, lower_bound
|
||||
|
||||
def forward(self, x) -> torch.Tensor:
|
||||
return x[:, :1] * 0. + self.layer(self.value) * (self.ub - self.lb) + self.lb
|
||||
|
||||
def get_value(self) -> torch.Tensor:
|
||||
return self.layer(self.value) * (self.ub - self.lb) + self.lb
|
||||
|
||||
|
||||
class Arch(enum.Enum):
|
||||
"""Enumerate pre-defined neural networks."""
|
||||
|
||||
mlp = 'mlp'
|
||||
toy = 'toy'
|
||||
mlp_xl = 'mlp_xl'
|
||||
single_var = 'single_var'
|
||||
bounded_single_var = 'bounded_single_var'
|
||||
siren = 'siren'
|
||||
|
||||
|
||||
def get_net_node(inputs: Union[Tuple[str, ...], List[str]], outputs: Union[Tuple[str, ...], List[str]],
|
||||
arch: Arch = None, name=None,
|
||||
*args,
|
||||
**kwargs) -> NetNode:
|
||||
"""Get a net node wrapping networks with pre-defined configurations
|
||||
|
||||
:param inputs: Input symbols for the generated node.
|
||||
:type inputs: Union[Tuple[str, ...]
|
||||
:param outputs: Output symbols for the generated node.
|
||||
:type outputs: Union[Tuple[str, ...]
|
||||
:param arch: One can choose one of
|
||||
- Arch.mlp
|
||||
- Arch.mlp_xl(more layers and more neurons)
|
||||
- Arch.single_var
|
||||
- Arch.bounded_single_var
|
||||
:type arch: Arch
|
||||
:param name: The name of the generated node.
|
||||
:type name: str
|
||||
:param args:
|
||||
:param kwargs:
|
||||
:return:
|
||||
"""
|
||||
arch = Arch.mlp if arch is None else arch
|
||||
if 'evaluate' in kwargs.keys():
|
||||
evaluate = kwargs.pop('evaluate')
|
||||
else:
|
||||
if arch == Arch.mlp:
|
||||
seq = kwargs['seq'] if 'seq' in kwargs.keys() else [len(inputs), 20, 20, 20, 20, len(outputs)]
|
||||
evaluate = MLP(n_seq=seq, activation=Activation.swish, initialization=Initializer.kaiming_uniform,
|
||||
weight_norm=True)
|
||||
elif arch == Arch.toy:
|
||||
evaluate = SimpleExpr("nothing")
|
||||
elif arch == Arch.mlp_xl or arch == 'fc':
|
||||
seq = kwargs['seq'] if 'seq' in kwargs.keys() else [len(inputs), 512, 512, 512, 512, 512, 512, len(outputs)]
|
||||
evaluate = MLP(n_seq=seq, activation=Activation.silu, initialization=Initializer.kaiming_uniform,
|
||||
weight_norm=True)
|
||||
elif arch == Arch.single_var:
|
||||
evaluate = SingleVar(initialization=kwargs.get('initialization', 1.))
|
||||
elif arch == Arch.bounded_single_var:
|
||||
evaluate = BoundedSingleVar(lower_bound=kwargs['lower_bound'], upper_bound=kwargs['upper_bound'])
|
||||
elif arch == Arch.siren:
|
||||
seq = kwargs['seq'] if 'seq' in kwargs.keys() else [len(inputs), 512, 512, 512, 512, 512, 512, len(outputs)]
|
||||
evaluate = Siren(n_seq=seq)
|
||||
else:
|
||||
logger.error(f'{arch} is not supported!')
|
||||
raise NotImplementedError(f'{arch} is not supported!')
|
||||
nn = NetNode(inputs=inputs, outputs=outputs, net=evaluate, name=name, *args, **kwargs)
|
||||
return nn
|
||||
|
||||
|
||||
def get_shared_net_node(shared_node: NetNode, inputs: Union[Tuple[str, ...], List[str]],
|
||||
outputs: Union[Tuple[str, ...], List[str]], name=None, *args,
|
||||
**kwargs) -> NetNode:
|
||||
"""Construct a netnode, the net of which is shared by a given netnode. One can specify different inputs and outputs
|
||||
just like an independent netnode. However, the net parameters may have multiple references. Thus the step
|
||||
operations during optimization should only be applied once.
|
||||
|
||||
:param shared_node: An existing netnode, the network of which will be shared.
|
||||
:type shared_node: NetNode
|
||||
:param inputs: Input symbols for the generated node.
|
||||
:type inputs: Union[Tuple[str, ...]
|
||||
:param outputs: Output symbols for the generated node.
|
||||
:type outputs: Union[Tuple[str, ...]
|
||||
:param name: The name of the generated node.
|
||||
:type name: str
|
||||
:param args:
|
||||
:param kwargs:
|
||||
:return:
|
||||
"""
|
||||
nn = NetNode(inputs, outputs, shared_node.net, is_reference=True, name=name, *args, **kwargs)
|
||||
return nn
|
||||
|
||||
|
||||
def get_inter_name(length: int, prefix: str):
|
||||
return [prefix + f'_{i}' for i in range(length)]
|
||||
|
||||
|
||||
class SimpleExpr(torch.nn.Module):
|
||||
"""This class is for testing. One can override SimpleExper.forward to represent complex formulas."""
|
||||
|
||||
def __init__(self, expr, name='expr'):
|
||||
super().__init__()
|
||||
self.evaluate = expr
|
||||
self.name = name
|
||||
self._placeholder = torch.nn.Parameter(torch.Tensor([0.0]))
|
||||
|
||||
def forward(self, x):
|
||||
return self._placeholder + x[:, :1] * x[:, :1] / 2 + x[:, 1:] * x[:, 1:] / 2 - self._placeholder
|
||||
|
|
@ -0,0 +1,71 @@
|
|||
"""Basic Callback classes"""
|
||||
|
||||
import os
|
||||
import pathlib
|
||||
from typing import Dict
|
||||
from torch.utils.tensorboard import SummaryWriter
|
||||
from idrlnet.receivers import Receiver, Signal
|
||||
from idrlnet.variable import Variables
|
||||
|
||||
__all__ = ['GradientReceiver', 'SummaryReceiver', 'HandleResultReceiver']
|
||||
|
||||
|
||||
class GradientReceiver(Receiver):
|
||||
"""Register the receiver to monitor gradient norm on the Tensorboard."""
|
||||
|
||||
def receive_notify(self, solver: 'Solver', message):
|
||||
if not (Signal.TRAIN_PIPE_END in message):
|
||||
return
|
||||
for netnode in solver.netnodes:
|
||||
if not netnode.require_no_grad:
|
||||
model = netnode.net
|
||||
total_norm = 0
|
||||
for p in model.parameters():
|
||||
param_norm = p.grad.data.norm(2)
|
||||
total_norm += param_norm.item() ** 2
|
||||
total_norm = total_norm ** (1. / 2)
|
||||
assert isinstance(solver.receivers[0], SummaryWriter)
|
||||
solver.summary_receiver.add_scalar('gradient/total_norm', total_norm, solver.global_step)
|
||||
|
||||
|
||||
class SummaryReceiver(SummaryWriter, Receiver):
|
||||
"""The receiver will be automatically registered to control the Tensorboard."""
|
||||
|
||||
def __init__(self, *args, **kwargs):
|
||||
SummaryWriter.__init__(self, *args, **kwargs)
|
||||
|
||||
def receive_notify(self, solver: 'Solver', message: Dict):
|
||||
if Signal.AFTER_COMPUTE_LOSS in message.keys():
|
||||
loss_component = message[Signal.AFTER_COMPUTE_LOSS]
|
||||
self.add_scalars('loss_overview', loss_component, solver.global_step)
|
||||
for key, value in loss_component.items():
|
||||
self.add_scalar(f'loss_component/{key}', value, solver.global_step)
|
||||
if Signal.TRAIN_PIPE_END in message.keys():
|
||||
for i, optimizer in enumerate(solver.optimizers):
|
||||
self.add_scalar(f'optimizer/lr_{i}', optimizer.param_groups[0]['lr'], solver.global_step)
|
||||
|
||||
|
||||
class HandleResultReceiver(Receiver):
|
||||
"""The receiver will be automatically registered to save results on training domains."""
|
||||
|
||||
def __init__(self, result_dir):
|
||||
self.result_dir = result_dir
|
||||
|
||||
def receive_notify(self, solver: 'Solver', message: Dict):
|
||||
if Signal.SOLVE_END in message.keys():
|
||||
samples = solver.sample_variables_from_domains()
|
||||
in_var, _, lambda_out = solver.generate_in_out_dict(samples)
|
||||
pred_out_sample = solver.forward_through_all_graph(in_var, solver.outvar_dict_index)
|
||||
diff_out_sample = {key: Variables() for key in pred_out_sample}
|
||||
results_path = pathlib.Path(self.result_dir)
|
||||
results_path.mkdir(exist_ok=True, parents=True)
|
||||
for key in samples:
|
||||
for _key in samples[key]:
|
||||
if _key not in pred_out_sample[key].keys():
|
||||
pred_out_sample[key][_key] = samples[key][_key]
|
||||
diff_out_sample[key][_key] = samples[key][_key]
|
||||
else:
|
||||
diff_out_sample[key][_key] = pred_out_sample[key][_key] - samples[key][_key]
|
||||
samples[key].save(os.path.join(results_path, f'{key}_true'), ['vtu', 'np', 'csv'])
|
||||
pred_out_sample[key].save(os.path.join(results_path, f'{key}_pred'), ['vtu', 'np', 'csv'])
|
||||
diff_out_sample[key].save(os.path.join(results_path, f'{key}_diff'), ['vtu', 'np', 'csv'])
|
||||
|
|
@ -0,0 +1,182 @@
|
|||
"""Define DataNode"""
|
||||
|
||||
import numpy
|
||||
import torch
|
||||
import inspect
|
||||
import functools
|
||||
import abc
|
||||
from typing import Callable, Tuple, List, Union
|
||||
from idrlnet.variable import Variables
|
||||
from idrlnet.node import Node
|
||||
from idrlnet.geo_utils.sympy_np import lambdify_np
|
||||
from idrlnet.header import logger
|
||||
|
||||
|
||||
class DataNode(Node):
|
||||
"""A class inherits node.Node. With sampling methods implemented, the instance will generate sample points.
|
||||
|
||||
:param inputs: input keys in return.
|
||||
:type inputs: Union[Tuple[str, ...], List[str]]
|
||||
:param outputs: output keys in return.
|
||||
:type outputs: Union[Tuple[str, ...], List[str]]
|
||||
:param sample_fn: Callable instances for sampling. Implementation of SampleDomain is suggested for this arg.
|
||||
:type sample_fn: Callable
|
||||
:param loss_fn: Reduce the difference between a given data and this the output of the node to a simple scalar.
|
||||
square and L1 are implemented currently.
|
||||
defaults to 'square'.
|
||||
:type loss_fn: str
|
||||
:param lambda_outputs: Weight for each output in return, defaults to None.
|
||||
:type lambda_outputs: Union[Tuple[str,...], List[str]]
|
||||
:param name: The name of the node.
|
||||
:type name: str
|
||||
:param sigma: The weight for the whole node. defaults to 1.
|
||||
:type sigma: float
|
||||
:param var_sigma: whether automatical loss balance technique is used. defaults to false
|
||||
:type var_sigma: bool
|
||||
:param args:
|
||||
:param kwargs:
|
||||
"""
|
||||
counter = 0
|
||||
|
||||
@property
|
||||
def sample_fn(self):
|
||||
return self._sample_fn
|
||||
|
||||
@sample_fn.setter
|
||||
def sample_fn(self, sample_fn):
|
||||
self._sample_fn = sample_fn
|
||||
|
||||
@property
|
||||
def loss_fn(self):
|
||||
return self._loss_function
|
||||
|
||||
@loss_fn.setter
|
||||
def loss_fn(self, loss_fn):
|
||||
self._loss_function = loss_fn
|
||||
|
||||
@property
|
||||
def lambda_outputs(self):
|
||||
return self._lambda_outputs
|
||||
|
||||
@lambda_outputs.setter
|
||||
def lambda_outputs(self, lambda_outputs):
|
||||
self._lambda_outputs = lambda_outputs
|
||||
|
||||
@property
|
||||
def sigma(self):
|
||||
"""A weight for the domain."""
|
||||
return self._sigma
|
||||
|
||||
@sigma.setter
|
||||
def sigma(self, sigma):
|
||||
self._sigma = sigma
|
||||
|
||||
def sample(self) -> Variables:
|
||||
"""Sample a group of points, represented by Variables.
|
||||
|
||||
:return: a group of points.
|
||||
:rtype: Variables
|
||||
"""
|
||||
input_vars, output_vars = self.sample_fn()
|
||||
for key, value in output_vars.items():
|
||||
if isinstance(value, torch.Tensor):
|
||||
pass
|
||||
elif isinstance(value, numpy.ndarray):
|
||||
pass
|
||||
else:
|
||||
try:
|
||||
output_vars[key] = lambdify_np(value, input_vars)(**input_vars)
|
||||
except:
|
||||
logger.error('unsupported constraints type.')
|
||||
raise ValueError('unsupported constraints type.')
|
||||
|
||||
try:
|
||||
return Variables({**input_vars, **output_vars}).to_torch_tensor_()
|
||||
except:
|
||||
return Variables({**input_vars, **output_vars})
|
||||
|
||||
def __init__(self, inputs: Union[Tuple[str, ...], List[str]], outputs: Union[Tuple[str, ...], List[str]],
|
||||
sample_fn: Callable, loss_fn: str = 'square', lambda_outputs: Union[Tuple[str, ...], List[str]] = None,
|
||||
name=None, sigma=1.0, var_sigma=False,
|
||||
*args, **kwargs):
|
||||
self.inputs: Union[Tuple, List[str]] = inputs
|
||||
self.outputs: Union[Tuple, List[str]] = outputs
|
||||
self.lambda_outputs = lambda_outputs
|
||||
if name is not None:
|
||||
self.name = name
|
||||
else:
|
||||
self.name: str = "Domain_{}".format(self.counter)
|
||||
type(self).counter += 1
|
||||
self.sigma = sigma
|
||||
self.sigma = torch.tensor(sigma, dtype=torch.float32, requires_grad=var_sigma)
|
||||
self.sample_fn: Callable = sample_fn
|
||||
self.loss_fn = loss_fn
|
||||
|
||||
def __str__(self):
|
||||
str_list = ["DataNode properties:\n"
|
||||
"lambda_outputs: {}\n".format(self.lambda_outputs)]
|
||||
return super().__str__() + ''.join(str_list)
|
||||
|
||||
|
||||
def get_data_node(fun: Callable, name=None, loss_fn='square', sigma=1., var_sigma=False, *args, **kwargs) -> DataNode:
|
||||
""" Construct a datanode from sampling functions.
|
||||
|
||||
:param fun: Each call of the Callable object should return a sampling dict.
|
||||
:type fun: Callable
|
||||
:param name: name of the generated Datanode, defaults to None
|
||||
:type name: str
|
||||
:param loss_fn: Specify a loss function for the data node.
|
||||
:type loss_fn: str
|
||||
:param args:
|
||||
:param kwargs:
|
||||
:return: An instance of Datanode
|
||||
:rtype: DataNode
|
||||
"""
|
||||
in_, out_ = fun()
|
||||
inputs = list(in_.keys())
|
||||
outputs = list(out_.keys())
|
||||
lambda_outputs = list(filter(lambda x: x.startswith('lambda_'), outputs))
|
||||
outputs = list(filter(lambda x: not x.startswith('lambda_'), outputs))
|
||||
name = (fun.__name__ if inspect.isfunction(fun) else type(fun).__name__) if name is None else name
|
||||
dn = DataNode(inputs=inputs, outputs=outputs, sample_fn=fun, lambda_outputs=lambda_outputs, loss_fn=loss_fn,
|
||||
name=name, sigma=sigma, var_sigma=var_sigma, *args, **kwargs)
|
||||
return dn
|
||||
|
||||
|
||||
def datanode(_fun: Callable = None, name=None, loss_fn='square', sigma=1., var_sigma=False, **kwargs):
|
||||
"""As an alternative, decorate Callable classes as Datanode."""
|
||||
|
||||
def wrap(fun):
|
||||
if inspect.isclass(fun):
|
||||
assert issubclass(fun, SampleDomain), f"{fun} should be subclass of .data.Sample"
|
||||
fun = fun()
|
||||
assert isinstance(fun, Callable)
|
||||
|
||||
@functools.wraps(fun)
|
||||
def wrapped_fun():
|
||||
dn = get_data_node(fun, name=name, loss_fn=loss_fn, sigma=sigma, var_sigma=var_sigma, **kwargs)
|
||||
return dn
|
||||
|
||||
return wrapped_fun
|
||||
|
||||
return wrap if _fun is None else wrap(_fun)
|
||||
|
||||
|
||||
def get_data_nodes(funs: List[Callable], *args, **kwargs) -> Tuple[DataNode]:
|
||||
if 'names' in kwargs:
|
||||
names = kwargs.pop('names')
|
||||
return tuple(get_data_node(fun, name=name, *args, **kwargs) for fun, name in zip(funs, names))
|
||||
else:
|
||||
return tuple(get_data_node(fun, *args, **kwargs) for fun in funs)
|
||||
|
||||
|
||||
class SampleDomain(metaclass=abc.ABCMeta):
|
||||
"""Template for Callable sampling function."""
|
||||
|
||||
@abc.abstractmethod
|
||||
def sampling(self, *args, **kwargs):
|
||||
"""The method returns sampling points"""
|
||||
raise NotImplementedError(f"{type(self)}.sampling method not implemented")
|
||||
|
||||
def __call__(self, *args, **kwargs):
|
||||
return self.sampling(self, *args, **kwargs)
|
||||
|
|
@ -0,0 +1,3 @@
|
|||
from .geo_builder import GeometryBuilder
|
||||
from .geo_obj import *
|
||||
from .sympy_np import *
|
||||
|
|
@ -0,0 +1,347 @@
|
|||
"""This module defines basic behaviour of Geometric Objects."""
|
||||
import abc
|
||||
import collections
|
||||
import copy
|
||||
import itertools
|
||||
from functools import reduce
|
||||
from typing import Dict, List, Union, Tuple
|
||||
import numpy as np
|
||||
from sympy import cos, sin, Symbol
|
||||
import math
|
||||
|
||||
from idrlnet.geo_utils.sympy_np import lambdify_np, WrapMax, WrapMul, WrapMin
|
||||
|
||||
|
||||
class CheckMeta(type):
|
||||
"""Make sure that elements are checked when an instance is created,"""
|
||||
|
||||
def __call__(cls, *args, **kwargs):
|
||||
obj = type.__call__(cls, *args, **kwargs)
|
||||
obj.check_elements()
|
||||
return obj
|
||||
|
||||
|
||||
class AbsGeoObj(metaclass=abc.ABCMeta):
|
||||
@abc.abstractmethod
|
||||
def rotation(self, angle: float, axis: str = 'z'):
|
||||
pass
|
||||
|
||||
@abc.abstractmethod
|
||||
def scaling(self, scale: float):
|
||||
pass
|
||||
|
||||
@abc.abstractmethod
|
||||
def translation(self, direction):
|
||||
pass
|
||||
|
||||
|
||||
class Edge(AbsGeoObj):
|
||||
def __init__(self, functions, ranges: Dict, area):
|
||||
self.functions = functions
|
||||
self.ranges = ranges
|
||||
self.area = area
|
||||
|
||||
@property
|
||||
def axes(self) -> List[str]:
|
||||
return [key for key in self.functions if not key.startswith('normal')]
|
||||
|
||||
def rotation(self, angle: float, axis: str = 'z'):
|
||||
assert len(self.axes) > 1, 'Cannot rotate a object with dim<2'
|
||||
rotated_dims = [key for key in self.axes if key != axis]
|
||||
rd1, rd2, n = rotated_dims[0], rotated_dims[1], 'normal_'
|
||||
self.functions[rd1] = (cos(angle) * self.functions[rd1] - sin(angle) * self.functions[rd2])
|
||||
self.functions[n + rd1] = cos(angle) * self.functions[n + rd1] - sin(angle) * self.functions[n + rd2]
|
||||
self.functions[rd2] = (sin(angle) * self.functions[rd1] + cos(angle) * self.functions[rd2])
|
||||
self.functions[n + rd2] = sin(angle) * self.functions[n + rd1] + cos(angle) * self.functions[n + rd2]
|
||||
return self
|
||||
|
||||
def scaling(self, scale: float):
|
||||
for key in self.axes:
|
||||
self.functions[key] *= scale
|
||||
self.area = scale ** (len(self.axes) - 1) * self.area
|
||||
return self
|
||||
|
||||
def translation(self, direction):
|
||||
assert len(direction) == len(self.axes), 'Moving direction must have the save dimension with the object'
|
||||
for key, x in zip(self.axes, direction):
|
||||
self.functions[key] += x
|
||||
return self
|
||||
|
||||
def sample(self, density: int, param_ranges=None, low_discrepancy=False) -> Dict[str, np.ndarray]:
|
||||
param_ranges = {} if param_ranges is None else param_ranges
|
||||
inputs = {**self.ranges, **param_ranges}.keys()
|
||||
area_fn = lambdify_np(self.area, inputs)
|
||||
param_points = _ranged_sample(100, ranges={**self.ranges, **param_ranges})
|
||||
nr_points = int(density * (np.mean(area_fn(**param_points))))
|
||||
|
||||
lambdify_functions = {'area': lambda **x: area_fn(**x) / next(iter(x.values())).shape[0]}
|
||||
param_points = _ranged_sample(nr_points, {**self.ranges, **param_ranges}, low_discrepancy)
|
||||
data_var = {}
|
||||
|
||||
for key, function in self.functions.items():
|
||||
lambdify_functions[key] = lambdify_np(function, inputs)
|
||||
|
||||
for key, function in lambdify_functions.items():
|
||||
assert callable(function)
|
||||
data_var[key] = function(**param_points)
|
||||
|
||||
for key in param_ranges:
|
||||
key = key if isinstance(key, str) else key.name
|
||||
data_var[key] = param_points[key]
|
||||
|
||||
return data_var
|
||||
|
||||
|
||||
class AbsCheckMix(abc.ABCMeta, CheckMeta):
|
||||
pass
|
||||
|
||||
|
||||
class Geometry(AbsGeoObj, metaclass=AbsCheckMix):
|
||||
edges: List[Edge] = None
|
||||
bounds: Dict = None
|
||||
sdf = None
|
||||
|
||||
def check_elements(self):
|
||||
if type(self) in [Geometry, Geometry1D, Geometry2D, Geometry3D]:
|
||||
return
|
||||
if self.edges is None:
|
||||
raise NotImplementedError('Geometry must define edges')
|
||||
if self.bounds is None:
|
||||
raise NotImplementedError('Geometry must define bounds')
|
||||
if self.sdf is None:
|
||||
raise NotImplementedError('Geometry must define sdf')
|
||||
|
||||
@property
|
||||
def axes(self) -> List[str]:
|
||||
return self.edges[0].axes
|
||||
|
||||
def translation(self, direction: Union[List, Tuple]) -> 'Geometry':
|
||||
assert len(direction) == len(self.axes)
|
||||
[edge.translation(direction) for edge in self.edges]
|
||||
self.sdf = self.sdf.subs([(Symbol(dim), Symbol(dim) - x) for dim, x in zip(self.axes, direction)])
|
||||
self.bounds = {dim: (self.bounds[dim][0] + x, self.bounds[dim][1] + x) for dim, x in zip(self.axes, direction)}
|
||||
return self
|
||||
|
||||
def rotation(self, angle: float, axis: str = 'z', center=None) -> 'Geometry':
|
||||
if center is not None:
|
||||
self.translation([-x for x in center])
|
||||
|
||||
[edge.rotation(angle, axis) for edge in self.edges]
|
||||
rotated_dims = [key for key in self.axes if key != axis]
|
||||
sp_0 = Symbol(rotated_dims[0])
|
||||
_sp_0 = Symbol('tmp_0')
|
||||
sp_1 = Symbol(rotated_dims[1])
|
||||
_sp_1 = Symbol('tmp_1')
|
||||
self.sdf = self.sdf.subs({sp_0: cos(angle) * _sp_0 + sin(angle) * _sp_1,
|
||||
sp_1: - sin(angle) * _sp_0 + cos(angle) * _sp_1})
|
||||
self.sdf = self.sdf.subs({_sp_0: sp_0, _sp_1: sp_1})
|
||||
self.bounds[rotated_dims[0]], self.bounds[rotated_dims[1]] = _rotate_rec(self.bounds[rotated_dims[0]],
|
||||
self.bounds[rotated_dims[1]],
|
||||
angle=angle)
|
||||
if center is not None:
|
||||
self.translation(center)
|
||||
return self
|
||||
|
||||
def scaling(self, scale: float, center: Tuple = None) -> 'Geometry':
|
||||
assert scale > 0, 'scaling must be positive'
|
||||
if center is not None:
|
||||
self.translation(tuple([-x for x in center]))
|
||||
[edge.scaling(scale) for edge in self.edges]
|
||||
self.sdf = self.sdf.subs({Symbol(dim): Symbol(dim) / scale for dim in self.axes})
|
||||
self.sdf = scale * self.sdf
|
||||
for dim in self.axes:
|
||||
self.bounds[dim] = (self.bounds[dim][0] * scale, self.bounds[dim][1] * scale)
|
||||
if center is not None:
|
||||
self.translation(center)
|
||||
return self
|
||||
|
||||
def duplicate(self) -> 'Geometry':
|
||||
return copy.deepcopy(self)
|
||||
|
||||
def sample_boundary(self, density: int, sieve=None, param_ranges: Dict = None, low_discrepancy=False) -> Dict[
|
||||
str, np.ndarray]:
|
||||
param_ranges = dict() if param_ranges is None else param_ranges
|
||||
points_list = [edge.sample(density, param_ranges, low_discrepancy) for edge in
|
||||
self.edges]
|
||||
points = reduce(lambda e1, e2: {_k: np.concatenate([e1[_k], e2[_k]], axis=0) for _k in e1}, points_list)
|
||||
points = self._sieve_points(points, sieve, sign=-1, tol=1e-4)
|
||||
return points
|
||||
|
||||
def _sieve_points(self, points, sieve, tol=1e-4, sign=1.):
|
||||
|
||||
sdf_fn = lambdify_np(self.sdf, points.keys())
|
||||
points['sdf'] = sdf_fn(**points)
|
||||
|
||||
criteria_fn = lambdify_np(True if sieve is None else sieve, points.keys())
|
||||
criteria_index = np.logical_and(np.greater(points['sdf'], -tol), criteria_fn(**points))
|
||||
if sign == -1:
|
||||
criteria_index = np.logical_and(np.less(points['sdf'], tol), criteria_index)
|
||||
points = {k: v[criteria_index[:, 0], :] for k, v in points.items()}
|
||||
return points
|
||||
|
||||
def sample_interior(self, density: int, bounds: Dict = None, sieve=None, param_ranges: Dict = None,
|
||||
low_discrepancy=False) -> Dict[str, np.ndarray]:
|
||||
bounds = self.bounds if bounds is None else bounds
|
||||
bounds = {Symbol(key) if isinstance(key, str) else key: value for key, value in bounds.items()}
|
||||
param_ranges = {} if param_ranges is None else param_ranges
|
||||
measure = np.prod([value[1] - value[0] for value in bounds.values()])
|
||||
nr_points = int(measure * density)
|
||||
|
||||
points = _ranged_sample(nr_points, {**bounds, **param_ranges}, low_discrepancy=low_discrepancy)
|
||||
assert len(points.keys()) >= 0, "No points have been sampled!"
|
||||
|
||||
points = self._sieve_points(points, sieve, tol=0.)
|
||||
|
||||
points['area'] = np.zeros_like(points['sdf']) + (1.0 / density)
|
||||
return points
|
||||
|
||||
def __add__(self, other: 'Geometry') -> 'Geometry':
|
||||
geo = self.generate_geo_obj(other)
|
||||
geo.edges = self.edges + other.edges
|
||||
geo.sdf = WrapMax(self.sdf, other.sdf)
|
||||
geo.bounds = dict()
|
||||
for key, value in self.bounds.items():
|
||||
geo.bounds[key] = (
|
||||
min(other.bounds[key][0], self.bounds[key][0]), max(other.bounds[key][1], self.bounds[key][1]))
|
||||
return geo
|
||||
|
||||
def generate_geo_obj(self, other=None):
|
||||
if isinstance(self, Geometry1D):
|
||||
geo = Geometry1D()
|
||||
assert isinstance(other, Geometry1D) or other is None
|
||||
elif isinstance(self, Geometry2D):
|
||||
geo = Geometry2D()
|
||||
assert isinstance(other, Geometry2D) or other is None
|
||||
elif isinstance(self, Geometry3D):
|
||||
geo = Geometry3D()
|
||||
assert isinstance(other, Geometry3D) or other is None
|
||||
else:
|
||||
raise TypeError
|
||||
return geo
|
||||
|
||||
def __sub__(self, other: 'Geometry') -> 'Geometry':
|
||||
geo = self.generate_geo_obj(other)
|
||||
|
||||
geo.edges = self.edges + [_inverse_edge(edge) for edge in other.edges]
|
||||
geo.sdf = WrapMin(self.sdf, WrapMul(-1, other.sdf))
|
||||
geo.bounds = dict()
|
||||
for key, value in self.bounds.items():
|
||||
geo.bounds[key] = (self.bounds[key][0], self.bounds[key][1])
|
||||
return geo
|
||||
|
||||
def __invert__(self) -> 'Geometry':
|
||||
geo = self.generate_geo_obj()
|
||||
geo.edges = [_inverse_edge(edge) for edge in self.edges]
|
||||
geo.sdf = WrapMul(-1, self.sdf)
|
||||
for key, value in self.bounds.items():
|
||||
geo.bounds[key] = (-float('inf'), float('inf'))
|
||||
return geo
|
||||
|
||||
def __and__(self, other: 'Geometry') -> 'Geometry':
|
||||
geo = self.generate_geo_obj(other)
|
||||
geo.edges = self.edges + other.edges
|
||||
geo.sdf = WrapMin(self.sdf, other.sdf)
|
||||
geo.bounds = dict()
|
||||
for key, value in self.bounds.items():
|
||||
geo.bounds[key] = (
|
||||
max(other.bounds[key][0], self.bounds[key][0]), min(other.bounds[key][1], self.bounds[key][1]))
|
||||
return geo
|
||||
|
||||
|
||||
class Geometry1D(Geometry):
|
||||
pass
|
||||
|
||||
|
||||
class Geometry2D(Geometry):
|
||||
pass
|
||||
|
||||
|
||||
class Geometry3D(Geometry):
|
||||
pass
|
||||
|
||||
|
||||
# todo: sample in cuda device
|
||||
def _ranged_sample(batch_size: int, ranges: Dict, low_discrepancy: bool = False) -> Dict[str, np.ndarray]:
|
||||
points = dict()
|
||||
low_discrepancy_stack = []
|
||||
for key, value in ranges.items():
|
||||
if isinstance(value, (float, int)):
|
||||
samples = np.ones((batch_size, 1)) * value
|
||||
elif isinstance(value, tuple):
|
||||
assert len(value) == 2, 'Tuple: length of range should be 2!'
|
||||
if low_discrepancy:
|
||||
low_discrepancy_stack.append((key.name, value))
|
||||
continue
|
||||
else:
|
||||
samples = np.random.uniform(value[0], value[1], size=(batch_size, 1))
|
||||
elif isinstance(value, collections.Callable):
|
||||
samples = value(batch_size)
|
||||
else:
|
||||
raise TypeError(f'range type {type(value)} not supported!')
|
||||
points[key.name] = samples
|
||||
if low_discrepancy:
|
||||
low_discrepancy_points_dict = _low_discrepancy_sampling(batch_size, low_discrepancy_stack)
|
||||
points.update(low_discrepancy_points_dict)
|
||||
for key, v in points.items():
|
||||
points[key] = v.astype(np.float64)
|
||||
return points
|
||||
|
||||
|
||||
def _rotate_rec(x: Tuple, y: Tuple, angle: float):
|
||||
points = itertools.product(x, y)
|
||||
min_x, min_y = float('inf'), float('inf')
|
||||
max_x, max_y = -float('inf'), -float('inf')
|
||||
try:
|
||||
for x, y in points:
|
||||
new_x = cos(angle) * x - sin(angle) * y
|
||||
new_y = sin(angle) * x + cos(angle) * y
|
||||
min_x = min(new_x, min_x)
|
||||
min_y = min(new_y, min_y)
|
||||
max_x = max(new_x, max_x)
|
||||
max_y = max(new_y, max_y)
|
||||
except TypeError:
|
||||
angle = math.pi / 4
|
||||
for x, y in points:
|
||||
new_x = cos(angle) * x - sin(angle) * y
|
||||
new_y = sin(angle) * x + cos(angle) * y
|
||||
min_x = min(new_x, min_x)
|
||||
min_y = min(new_y, min_y)
|
||||
max_x = max(new_x, max_x)
|
||||
max_y = max(new_y, max_y)
|
||||
return (min_x, max_x), (min_y, max_y)
|
||||
|
||||
|
||||
def _low_discrepancy_sampling(n_points, low_discrepancy_stack: List[Tuple]):
|
||||
dim = len(low_discrepancy_stack)
|
||||
sections = 2 ** dim
|
||||
|
||||
def uniform(x, start, end, rmin, bi_range=0.5):
|
||||
dims = len(rmin)
|
||||
if end - start <= 1:
|
||||
return
|
||||
d, r = (end - start) // sections, (end - start) % sections
|
||||
r = (np.arange(sections - 1, 0, -1) + r) // sections
|
||||
np.random.shuffle(r)
|
||||
d = (d + r).cumsum() + start
|
||||
q = np.concatenate([np.array([start]), d, np.array([end])])
|
||||
|
||||
for i in range(len(q) - 1):
|
||||
for j in range(dims):
|
||||
x[q[i]:q[i + 1], j] = (x[q[i]:q[i + 1], j] - rmin[j]) / 2 + rmin[j] + ((i >> j) & 1) * bi_range
|
||||
rmin_sub = [v + bi_range * ((i >> j) & 1) for j, v in enumerate(rmin)]
|
||||
uniform(x, q[i], q[i + 1], rmin_sub, bi_range=bi_range / 2)
|
||||
return x
|
||||
|
||||
n = n_points
|
||||
points = np.random.rand(n, dim)
|
||||
uniform(points, start=0, end=n, rmin=[0] * dim)
|
||||
points_dict = {}
|
||||
for i, (key, bi_range) in enumerate(low_discrepancy_stack):
|
||||
points_dict[key] = points[:, i:i + 1] * (bi_range[1] - bi_range[0]) + bi_range[0]
|
||||
return points_dict
|
||||
|
||||
|
||||
def _inverse_edge(edge: Edge):
|
||||
new_functions = {k: -v if k.startswith('normal_') else v for k, v in edge.functions.items()}
|
||||
edge = Edge(functions=new_functions, ranges=edge.ranges, area=edge.area)
|
||||
return edge
|
||||
|
|
@ -0,0 +1,37 @@
|
|||
""" A simple factory for constructing Geometric Objects"""
|
||||
|
||||
from .geo import Geometry
|
||||
from .geo_obj import Line1D, Line, Tube2D, Rectangle, Circle, Plane, Tube3D, Box, Sphere, Cylinder, CircularTube, \
|
||||
Triangle, Heart
|
||||
|
||||
__all__ = ['GeometryBuilder']
|
||||
|
||||
|
||||
class GeometryBuilder:
|
||||
GEOMAP = {'Line1D': Line1D,
|
||||
'Line': Line,
|
||||
'Rectangle': Rectangle,
|
||||
'Circle': Circle,
|
||||
'Channel2D': Tube2D,
|
||||
'Plane': Plane,
|
||||
'Sphere': Sphere,
|
||||
'Box': Box,
|
||||
'Channel': Tube3D,
|
||||
'Channel3D': Tube3D,
|
||||
'Cylinder': Cylinder,
|
||||
'CircularTube': CircularTube,
|
||||
'Triangle': Triangle,
|
||||
'Heart': Heart,
|
||||
}
|
||||
|
||||
@staticmethod
|
||||
def get_geometry(geo: str, **kwargs) -> Geometry:
|
||||
"""Simple factory method for constructing geometry object.
|
||||
:param geo: Specified a string for geometry, which should be in GeometryBuilder.GEOMAP
|
||||
:rtype geo: str
|
||||
:param kwargs:
|
||||
:return: A geometry object with given kwargs.
|
||||
:rtype: Geometry
|
||||
"""
|
||||
assert geo in GeometryBuilder.GEOMAP.keys(), f'The geometry {geo} not implemented!'
|
||||
return GeometryBuilder.GEOMAP[geo](**kwargs)
|
||||
|
|
@ -0,0 +1,549 @@
|
|||
"""Concrete shape."""
|
||||
|
||||
import math
|
||||
from math import pi
|
||||
from typing import Union, List, Tuple
|
||||
import numpy as np
|
||||
from sympy import symbols, Abs, sqrt, Max, Min, cos, sin, log, sign, Heaviside
|
||||
from sympy.vector import CoordSys3D
|
||||
from .geo import Edge, Geometry1D, Geometry2D, Geometry3D
|
||||
|
||||
__all__ = ['Line1D', 'Line', 'Tube2D', 'Rectangle', 'Circle', 'Heart', 'Triangle', 'Polygon', 'Plane', 'Tube3D', 'Tube',
|
||||
'CircularTube', 'Box', 'Sphere', 'Cylinder']
|
||||
|
||||
|
||||
class Line1D(Geometry1D):
|
||||
|
||||
def __init__(self, point_1, point_2):
|
||||
x, none = symbols('x none')
|
||||
ranges = {none: (0, 1)}
|
||||
edge_1 = Edge(functions={'x': point_1,
|
||||
'normal_x': -1},
|
||||
area=1.0,
|
||||
ranges=ranges)
|
||||
edge_2 = Edge(functions={'x': point_2,
|
||||
'normal_x': 1},
|
||||
area=1.0,
|
||||
ranges=ranges)
|
||||
self.edges = [edge_1, edge_2]
|
||||
dist = point_2 - point_1
|
||||
center_x = point_1 + dist / 2
|
||||
self.sdf = dist / 2 - Abs(x - center_x)
|
||||
|
||||
self.bounds = {'x': (point_1, point_2)}
|
||||
|
||||
|
||||
class Line(Geometry2D):
|
||||
def __init__(self, point_1, point_2, normal=1):
|
||||
x, y, l = symbols('x y l')
|
||||
ranges = {l: (0, 1)}
|
||||
dist_x = point_2[0] - point_1[0]
|
||||
dist_y = point_2[1] - point_1[1]
|
||||
normal_vector = (-dist_y * normal, dist_x * normal)
|
||||
normal_norm = math.sqrt(normal_vector[0] ** 2 + normal_vector[1] ** 2)
|
||||
normal_vector = (normal_vector[0] / normal_norm, normal_vector[1] / normal_norm)
|
||||
line_1 = Edge(functions={'x': point_1[0] + l * dist_x,
|
||||
'y': point_1[1] + l * dist_y,
|
||||
'normal_x': normal_vector[0],
|
||||
'normal_y': normal_vector[1]},
|
||||
ranges=ranges,
|
||||
area=normal_norm)
|
||||
self.edges = [line_1]
|
||||
self.sdf = ((x - point_1[0]) * dist_y - (y - point_1[1]) * dist_x) / normal_norm
|
||||
self.bounds = {'x': (min(point_1[0], point_2[0]), max(point_1[0], point_2[0])),
|
||||
'y': (min(point_1[1], point_2[1]), max(point_1[1], point_2[1]))}
|
||||
|
||||
|
||||
class Tube2D(Geometry2D):
|
||||
|
||||
def __init__(self, point_1, point_2):
|
||||
l, y = symbols('l y')
|
||||
ranges = {l: (0, 1)}
|
||||
dist_x = point_2[0] - point_1[0]
|
||||
dist_y = point_2[1] - point_1[1]
|
||||
line_1 = Edge(functions={'x': l * dist_x + point_1[0],
|
||||
'y': point_1[1],
|
||||
'normal_x': 0,
|
||||
'normal_y': -1},
|
||||
ranges=ranges,
|
||||
area=dist_x)
|
||||
line_2 = Edge(functions={'x': l * dist_x + point_1[0],
|
||||
'y': point_2[1],
|
||||
'normal_x': 0,
|
||||
'normal_y': 1},
|
||||
ranges=ranges,
|
||||
area=dist_x)
|
||||
self.edges = [line_1, line_2]
|
||||
center_y = point_1[1] + (dist_y) / 2
|
||||
y_diff = Abs(y - center_y) - (point_2[1] - center_y)
|
||||
outside_distance = sqrt(Max(y_diff, 0) ** 2)
|
||||
inside_distance = Min(y_diff, 0)
|
||||
self.sdf = - (outside_distance + inside_distance)
|
||||
self.bounds = {'x': (min(point_1[0], point_2[0]), max(point_1[0], point_2[0])),
|
||||
'y': (min(point_1[1], point_2[1]), max(point_1[1], point_2[1]))}
|
||||
|
||||
|
||||
class Rectangle(Geometry2D):
|
||||
def __init__(self, point_1, point_2):
|
||||
l, x, y = symbols('l x y')
|
||||
ranges = {l: (0, 1)}
|
||||
dist_x = point_2[0] - point_1[0]
|
||||
dist_y = point_2[1] - point_1[1]
|
||||
|
||||
edge_1 = Edge(functions={'x': l * dist_x + point_1[0],
|
||||
'y': point_1[1],
|
||||
'normal_x': 0,
|
||||
'normal_y': -1},
|
||||
ranges=ranges,
|
||||
area=dist_x)
|
||||
edge_2 = Edge(functions={'x': point_2[0],
|
||||
'y': l * dist_y + point_1[1],
|
||||
'normal_x': 1,
|
||||
'normal_y': 0},
|
||||
ranges=ranges,
|
||||
area=dist_y)
|
||||
edge_3 = Edge(functions={'x': l * dist_x + point_1[0],
|
||||
'y': point_2[1],
|
||||
'normal_x': 0,
|
||||
'normal_y': 1},
|
||||
ranges=ranges,
|
||||
area=dist_x)
|
||||
edge_4 = Edge(functions={'x': point_1[0],
|
||||
'y': -l * dist_y + point_2[1],
|
||||
'normal_x': -1,
|
||||
'normal_y': 0},
|
||||
ranges=ranges,
|
||||
area=dist_y)
|
||||
self.edges = [edge_1, edge_2, edge_3, edge_4]
|
||||
center_x = point_1[0] + (dist_x) / 2
|
||||
center_y = point_1[1] + (dist_y) / 2
|
||||
x_diff = Abs(x - center_x) - (point_2[0] - center_x)
|
||||
y_diff = Abs(y - center_y) - (point_2[1] - center_y)
|
||||
outside_distance = sqrt(Max(x_diff, 0) ** 2 + Max(y_diff, 0) ** 2)
|
||||
inside_distance = Min(Max(x_diff, y_diff), 0)
|
||||
self.sdf = - (outside_distance + inside_distance)
|
||||
self.bounds = {'x': (min(point_1[0], point_2[0]), max(point_1[0], point_2[0])),
|
||||
'y': (min(point_1[1], point_2[1]), max(point_1[1], point_2[1]))}
|
||||
|
||||
|
||||
class Circle(Geometry2D):
|
||||
|
||||
def __init__(self, center, radius):
|
||||
theta, x, y = symbols('theta x y')
|
||||
ranges = {theta: (0, 2 * math.pi)}
|
||||
edge = Edge(functions={'x': center[0] + radius * cos(theta),
|
||||
'y': center[1] + radius * sin(theta),
|
||||
'normal_x': 1 * cos(theta),
|
||||
'normal_y': 1 * sin(theta)},
|
||||
ranges=ranges,
|
||||
area=2 * pi * radius)
|
||||
|
||||
self.edges = [edge]
|
||||
self.sdf = radius - sqrt((x - center[0]) ** 2 + (y - center[1]) ** 2)
|
||||
self.bounds = {'x': (center[0] - radius, center[0] + radius), 'y': (center[1] - radius, center[1] + radius)}
|
||||
|
||||
|
||||
class Heart(Geometry2D):
|
||||
def __init__(self, center=(0, 0.5), radius=0.5):
|
||||
c1, c2 = center
|
||||
theta, t, x, y = symbols('t theta x y')
|
||||
ranges = {theta: (0, math.pi), t: (0, 1)}
|
||||
edge_1 = Edge(functions={'x': center[0] - t * radius,
|
||||
'y': center[1] - (1 - t) * radius,
|
||||
'normal_x': -1.,
|
||||
'normal_y': -1.},
|
||||
ranges=ranges,
|
||||
area=math.sqrt(2) * radius)
|
||||
|
||||
edge_2 = Edge(functions={'x': center[0] + t * radius,
|
||||
'y': center[1] - (1 - t) * radius,
|
||||
'normal_x': 1.,
|
||||
'normal_y': -1.},
|
||||
ranges=ranges,
|
||||
area=math.sqrt(2) * radius)
|
||||
|
||||
edge_3 = Edge(functions={'x': center[0] - radius / 2 + radius / math.sqrt(2) * cos(math.pi / 4 * 5 - theta),
|
||||
'y': center[1] + radius / 2 + radius / math.sqrt(2) * sin(math.pi / 4 * 5 - theta),
|
||||
'normal_x': cos(math.pi / 4 * 5 - theta),
|
||||
'normal_y': sin(math.pi / 4 * 5 - theta)},
|
||||
ranges=ranges,
|
||||
area=math.sqrt(2) * radius * math.pi)
|
||||
|
||||
edge_4 = Edge(functions={'x': center[0] + radius / 2 + radius / math.sqrt(2) * cos(math.pi / 4 * 3 - theta),
|
||||
'y': center[1] + radius / 2 + radius / math.sqrt(2) * sin(math.pi / 4 * 3 - theta),
|
||||
'normal_x': cos(math.pi / 4 * 3 - theta),
|
||||
'normal_y': sin(math.pi / 4 * 3 - theta)},
|
||||
ranges=ranges,
|
||||
area=math.sqrt(2) * radius * math.pi)
|
||||
|
||||
self.edges = [edge_1, edge_2, edge_3, edge_4]
|
||||
x, y = symbols('x y')
|
||||
x = (x - c1) * 0.5 / radius
|
||||
y = (y - c2) * 0.5 / radius + 0.5
|
||||
part1 = Heaviside(Abs(x) + y - 1) * (sqrt((Abs(x) - 0.25) ** 2 + (y - 0.75) ** 2) - math.sqrt(2) / 4)
|
||||
part_i = 0.5 * Max(Abs(x) + y, 0)
|
||||
part2 = (1 - Heaviside(Abs(x) + y - 1)) * sign(Abs(x) - y) * Min(sqrt(Abs(x) ** 2 + (y - 1) ** 2),
|
||||
sqrt((Abs(x) - part_i) ** 2 + (
|
||||
y - part_i) ** 2))
|
||||
self.sdf = (-part1 - part2) * radius * 2
|
||||
self.bounds = {'x': (
|
||||
center[0] - 0.5 * radius - 0.5 * math.sqrt(2) * radius,
|
||||
center[0] + 0.5 * radius + 0.5 * math.sqrt(2) * radius),
|
||||
'y': (center[1] - radius, center[1] + 0.5 * radius + 0.5 * math.sqrt(2) * radius)}
|
||||
|
||||
|
||||
class Triangle(Geometry2D):
|
||||
def __init__(self, p0, p1, p2):
|
||||
x, y, t = symbols('x y t')
|
||||
N = CoordSys3D('N')
|
||||
P0 = p0[0] * N.i + p0[1] * N.j
|
||||
P1 = p1[0] * N.i + p1[1] * N.j
|
||||
P2 = p2[0] * N.i + p2[1] * N.j
|
||||
p = x * N.i + y * N.j
|
||||
e0, e1, e2 = P1 - P0, P2 - P1, P0 - P2
|
||||
v0, v1, v2 = p - P0, p - P1, p - P2
|
||||
pq0 = v0 - e0 * Max(Min(v0.dot(e0) / e0.dot(e0), 1), 0)
|
||||
pq1 = v1 - e1 * Max(Min(v1.dot(e1) / e1.dot(e1), 1), 0)
|
||||
pq2 = v2 - e2 * Max(Min(v2.dot(e2) / e2.dot(e2), 1), 0)
|
||||
s = sign(e0.dot(N.i) * e2.dot(N.j) - e0.dot(N.j) * e2.dot(N.i))
|
||||
|
||||
u = sqrt(Min(pq0.dot(pq0), pq1.dot(pq1), pq2.dot(pq2)))
|
||||
|
||||
v = Min(s * (v0.dot(N.i) * e0.dot(N.j) - v0.dot(N.j) * e0.dot(N.i)),
|
||||
s * (v1.dot(N.i) * e1.dot(N.j) - v1.dot(N.j) * e1.dot(N.i)),
|
||||
s * (v2.dot(N.i) * e2.dot(N.j) - v2.dot(N.j) * e2.dot(N.i)))
|
||||
self.sdf = u * sign(v)
|
||||
|
||||
l0 = sqrt(e0.dot(e0))
|
||||
l1 = sqrt(e1.dot(e1))
|
||||
l2 = sqrt(e2.dot(e2))
|
||||
ranges = {t: (0, 1)}
|
||||
in_out_sign = -sign(e0.cross(e1).dot(N.k))
|
||||
edge_1 = Edge(functions={'x': p1[0] + t * (p0[0] - p1[0]),
|
||||
'y': p1[1] + t * (p0[1] - p1[1]),
|
||||
'normal_x': (p0[1] - p1[1]) / l0 * in_out_sign,
|
||||
'normal_y': (p1[0] - p0[0]) / l0 * in_out_sign},
|
||||
ranges=ranges,
|
||||
area=l0)
|
||||
edge_2 = Edge(functions={'x': p2[0] + t * (p1[0] - p2[0]),
|
||||
'y': p2[1] + t * (p1[1] - p2[1]),
|
||||
'normal_x': (p1[1] - p2[1]) / l1 * in_out_sign,
|
||||
'normal_y': (p2[0] - p1[0]) / l1 * in_out_sign},
|
||||
ranges=ranges,
|
||||
area=l1)
|
||||
edge_3 = Edge(functions={'x': p0[0] + t * (p2[0] - p0[0]),
|
||||
'y': p0[1] + t * (p2[1] - p0[1]),
|
||||
'normal_x': (p2[1] - p0[1]) / l2 * in_out_sign,
|
||||
'normal_y': (p0[0] - p2[0]) / l2 * in_out_sign},
|
||||
ranges=ranges,
|
||||
area=l2)
|
||||
self.edges = [edge_1, edge_2, edge_3]
|
||||
self.bounds = {'x': (min(p0[0], p1[0], p2[0]), max(p0[0], p1[0], p2[0])),
|
||||
'y': (min(p0[1], p1[1], p2[1]), max(p0[1], p1[1], p2[1]))}
|
||||
|
||||
|
||||
class Polygon(Geometry2D):
|
||||
def __init__(self, points):
|
||||
v = points
|
||||
t = symbols('t')
|
||||
ranges = {t: (0, 1)}
|
||||
|
||||
def _sdf(x: np.ndarray, y: np.ndarray, **kwargs):
|
||||
s = np.ones_like(x)
|
||||
_points = np.concatenate([x, y], axis=1)
|
||||
d = ((np.array(v[0]) - _points) ** 2).sum(axis=1, keepdims=True)
|
||||
for i in range(len(v)):
|
||||
e = np.array(v[i - 1]) - np.array(v[i])
|
||||
w = _points - np.array(v[i])
|
||||
b = w - e * np.clip((w * e).sum(axis=1, keepdims=True) / (e * e).sum(), 0, 1)
|
||||
d = np.minimum(d, (b * b).sum(keepdims=True, axis=1))
|
||||
cond1 = _points[:, 1:] >= v[i][1]
|
||||
cond2 = _points[:, 1:] < v[i - 1][1]
|
||||
cond3 = e[0] * w[:, 1:] > e[1] * w[:, :1]
|
||||
inverse_idx1 = np.all([cond1, cond2, cond3], axis=0)
|
||||
inverse_idx2 = np.all([np.logical_not(cond1), np.logical_not(cond2), np.logical_not(cond3)], axis=0)
|
||||
inverse_idx = np.any([inverse_idx1, inverse_idx2], axis=0)
|
||||
s[inverse_idx] *= -1
|
||||
return -np.sqrt(d) * s
|
||||
|
||||
self.sdf = _sdf
|
||||
self.edges = []
|
||||
for i, _ in enumerate(points):
|
||||
length = math.sqrt((points[i - 1][0] - points[i][0]) ** 2 + (points[i - 1][1] - points[i][1]) ** 2)
|
||||
edge = Edge(functions={'x': points[i - 1][0] - t * (points[i - 1][0] - points[i][0]),
|
||||
'y': points[i - 1][1] - t * (points[i - 1][1] - points[i][1]),
|
||||
'normal_x': (points[i][1] - points[i - 1][1]) / length,
|
||||
'normal_y': (points[i - 1][0] - points[i][0]) / length},
|
||||
ranges=ranges,
|
||||
area=length)
|
||||
self.edges.append(edge)
|
||||
_p = iter(zip(*points))
|
||||
_p1 = next(_p)
|
||||
_p2 = next(_p)
|
||||
self.bounds = {'x': (min(_p1), max(_p1)),
|
||||
'y': (min(_p2), max(_p2))}
|
||||
|
||||
def translation(self, direction: Union[List, Tuple]):
|
||||
raise NotImplementedError
|
||||
|
||||
def rotation(self, angle: float, axis: str = 'z', center=None):
|
||||
raise NotImplementedError
|
||||
|
||||
def scaling(self, scale: float, center: Tuple = None):
|
||||
raise NotImplementedError
|
||||
|
||||
|
||||
class Plane(Geometry3D):
|
||||
|
||||
def __init__(self, point_1, point_2, normal):
|
||||
assert point_1[0] == point_2[0], "Points must have the same x coordinate"
|
||||
|
||||
x, y, z, s_1, s_2 = symbols('x y z s_1 s_2')
|
||||
center = (point_1[0] + (point_2[0] - point_1[0]) / 2,
|
||||
point_1[1] + (point_2[1] - point_1[1]) / 2,
|
||||
point_1[2] + (point_2[2] - point_1[2]) / 2)
|
||||
side_y = point_2[1] - point_1[1]
|
||||
side_z = point_2[2] - point_1[2]
|
||||
|
||||
ranges = {s_1: (-1, 1), s_2: (-1, 1)}
|
||||
edge = Edge(functions={'x': center[0],
|
||||
'y': center[1] + 0.5 * s_1 * side_y,
|
||||
'z': center[2] + 0.5 * s_2 * side_z,
|
||||
'normal_x': 1e-10 + normal, # TODO rm 1e-10
|
||||
'normal_y': 0,
|
||||
'normal_z': 0},
|
||||
ranges=ranges,
|
||||
area=side_y * side_z)
|
||||
self.edges = [edge]
|
||||
|
||||
self.sdf = normal * (center[0] - x)
|
||||
|
||||
self.bounds = {'x': (min(point_1[0], point_2[0]), max(point_1[0], point_2[0])),
|
||||
'y': (min(point_1[1], point_2[1]), max(point_1[1], point_2[1])),
|
||||
'z': (min(point_1[2], point_2[2]), max(point_1[2], point_2[2])), }
|
||||
|
||||
|
||||
class Tube3D(Geometry3D):
|
||||
|
||||
def __init__(self, point_1, point_2):
|
||||
x, y, z, s_1, s_2 = symbols('x y z s_1 s_2')
|
||||
center = (point_1[0] + (point_2[0] - point_1[0]) / 2,
|
||||
point_1[1] + (point_2[1] - point_1[1]) / 2,
|
||||
point_1[2] + (point_2[2] - point_1[2]) / 2)
|
||||
side_x = point_2[0] - point_1[0]
|
||||
side_y = point_2[1] - point_1[1]
|
||||
side_z = point_2[2] - point_1[2]
|
||||
|
||||
ranges = {s_1: (-1, 1), s_2: (-1, 1)}
|
||||
edge_1 = Edge(functions={'x': center[0] + 0.5 * s_1 * side_x,
|
||||
'y': center[1] + 0.5 * s_2 * side_y,
|
||||
'z': center[2] + 0.5 * side_z,
|
||||
'normal_x': 0,
|
||||
'normal_y': 0,
|
||||
'normal_z': 1},
|
||||
ranges=ranges,
|
||||
area=side_x * side_y)
|
||||
edge_2 = Edge(functions={'x': center[0] + 0.5 * s_1 * side_x,
|
||||
'y': center[1] + 0.5 * s_2 * side_y,
|
||||
'z': center[2] - 0.5 * side_z,
|
||||
'normal_x': 0,
|
||||
'normal_y': 0,
|
||||
'normal_z': -1},
|
||||
ranges=ranges,
|
||||
area=side_x * side_y)
|
||||
edge_3 = Edge(functions={'x': center[0] + 0.5 * s_1 * side_x,
|
||||
'y': center[1] + 0.5 * side_y,
|
||||
'z': center[2] + 0.5 * s_2 * side_z,
|
||||
'normal_x': 0,
|
||||
'normal_y': 1,
|
||||
'normal_z': 0},
|
||||
ranges=ranges,
|
||||
area=side_x * side_z)
|
||||
edge_4 = Edge(functions={'x': center[0] + 0.5 * s_1 * side_x,
|
||||
'y': center[1] - 0.5 * side_y,
|
||||
'z': center[2] + 0.5 * s_2 * side_z,
|
||||
'normal_x': 0,
|
||||
'normal_y': -1,
|
||||
'normal_z': 0},
|
||||
ranges=ranges,
|
||||
area=side_x * side_z)
|
||||
self.edges = [edge_1, edge_2, edge_3, edge_4]
|
||||
y_dist = Abs(y - center[1]) - 0.5 * side_y
|
||||
z_dist = Abs(z - center[2]) - 0.5 * side_z
|
||||
outside_distance = sqrt(Max(y_dist, 0) ** 2 + Max(z_dist, 0) ** 2)
|
||||
inside_distance = Min(Max(y_dist, z_dist), 0)
|
||||
self.sdf = - (outside_distance + inside_distance)
|
||||
|
||||
self.bounds = {'x': (min(point_1[0], point_2[0]), max(point_1[0], point_2[0])),
|
||||
'y': (min(point_1[1], point_2[1]), max(point_1[1], point_2[1])),
|
||||
'z': (min(point_1[2], point_2[2]), max(point_1[2], point_2[2])), }
|
||||
|
||||
|
||||
class Tube(Tube3D):
|
||||
def __init__(self, point_1, point_2):
|
||||
super(Tube, self).__init__(point_1, point_2)
|
||||
|
||||
|
||||
class CircularTube(Geometry3D):
|
||||
def __init__(self, center, radius, height):
|
||||
x, y, z, h, theta = symbols('x y z h theta')
|
||||
ranges = {h: (-1, 1), theta: (0, 2 * pi)}
|
||||
edge_1 = Edge(functions={'x': center[0] + radius * cos(theta),
|
||||
'y': center[1] + radius * sin(theta),
|
||||
'z': center[2] + 0.5 * h * height,
|
||||
'normal_x': 1 * cos(theta),
|
||||
'normal_y': 1 * sin(theta),
|
||||
'normal_z': 0},
|
||||
ranges=ranges,
|
||||
area=height * 2 * pi * radius)
|
||||
|
||||
self.edges = [edge_1]
|
||||
self.sdf = radius - sqrt((x - center[0]) ** 2 + (y - center[1]) ** 2)
|
||||
|
||||
self.bounds = {'x': (center[0] - radius, center[0] + radius),
|
||||
'y': (center[1] - radius, center[1] + radius),
|
||||
'z': (center[2] - height / 2, center[2] + height / 2)}
|
||||
|
||||
|
||||
class Box(Geometry3D):
|
||||
def __init__(self, point_1, point_2):
|
||||
x, y, z, s_1, s_2 = symbols('x y z s_1 s_2')
|
||||
center = (point_1[0] + (point_2[0] - point_1[0]) / 2,
|
||||
point_1[1] + (point_2[1] - point_1[1]) / 2,
|
||||
point_1[2] + (point_2[2] - point_1[2]) / 2)
|
||||
side_x = point_2[0] - point_1[0]
|
||||
side_y = point_2[1] - point_1[1]
|
||||
side_z = point_2[2] - point_1[2]
|
||||
|
||||
ranges = {s_1: (-1, 1), s_2: (-1, 1)}
|
||||
|
||||
self.bounds = {'x': (min(point_1[0], point_2[0]), max(point_1[0], point_2[0])),
|
||||
'y': (min(point_1[1], point_2[1]), max(point_1[1], point_2[1])),
|
||||
'z': (min(point_1[2], point_2[2]), max(point_1[2], point_2[2])), }
|
||||
|
||||
edge_1 = Edge(functions={'x': center[0] + 0.5 * s_1 * side_x,
|
||||
'y': center[1] + 0.5 * s_2 * side_y,
|
||||
'z': center[2] + 0.5 * side_z,
|
||||
'normal_x': 0,
|
||||
'normal_y': 0,
|
||||
'normal_z': 1},
|
||||
ranges=ranges,
|
||||
area=side_x * side_y)
|
||||
edge_2 = Edge(functions={'x': center[0] + 0.5 * s_1 * side_x,
|
||||
'y': center[1] + 0.5 * s_2 * side_y,
|
||||
'z': center[2] - 0.5 * side_z,
|
||||
'normal_x': 0,
|
||||
'normal_y': 0,
|
||||
'normal_z': -1},
|
||||
ranges=ranges,
|
||||
area=side_x * side_y)
|
||||
edge_3 = Edge(functions={'x': center[0] + 0.5 * s_1 * side_x,
|
||||
'y': center[1] + 0.5 * side_y,
|
||||
'z': center[2] + 0.5 * s_2 * side_z,
|
||||
'normal_x': 0,
|
||||
'normal_y': 1,
|
||||
'normal_z': 0},
|
||||
ranges=ranges,
|
||||
area=side_x * side_z)
|
||||
edge_4 = Edge(functions={'x': center[0] + 0.5 * s_1 * side_x,
|
||||
'y': center[1] - 0.5 * side_y,
|
||||
'z': center[2] + 0.5 * s_2 * side_z,
|
||||
'normal_x': 0,
|
||||
'normal_y': -1,
|
||||
'normal_z': 0},
|
||||
ranges=ranges,
|
||||
area=side_x * side_z)
|
||||
edge_5 = Edge(functions={'x': center[0] + 0.5 * side_x,
|
||||
'y': center[1] + 0.5 * s_1 * side_y,
|
||||
'z': center[2] + 0.5 * s_2 * side_z,
|
||||
'normal_x': 1,
|
||||
'normal_y': 0,
|
||||
'normal_z': 0},
|
||||
ranges=ranges,
|
||||
area=side_y * side_z)
|
||||
edge_6 = Edge(functions={'x': center[0] - 0.5 * side_x,
|
||||
'y': center[1] + 0.5 * s_1 * side_y,
|
||||
'z': center[2] + 0.5 * s_2 * side_z,
|
||||
'normal_x': -1,
|
||||
'normal_y': 0,
|
||||
'normal_z': 0},
|
||||
ranges=ranges,
|
||||
area=side_y * side_z)
|
||||
self.edges = [edge_1, edge_2, edge_3, edge_4, edge_5, edge_6]
|
||||
x_dist = Abs(x - center[0]) - 0.5 * side_x
|
||||
y_dist = Abs(y - center[1]) - 0.5 * side_y
|
||||
z_dist = Abs(z - center[2]) - 0.5 * side_z
|
||||
outside_distance = sqrt(Max(x_dist, 0) ** 2 + Max(y_dist, 0) ** 2 + Max(z_dist, 0) ** 2)
|
||||
inside_distance = Min(Max(x_dist, y_dist, z_dist), 0)
|
||||
self.sdf = - (outside_distance + inside_distance)
|
||||
self.bounds = {'x': (min(point_1[0], point_2[0]), max(point_1[0], point_2[0])),
|
||||
'y': (min(point_1[1], point_2[1]), max(point_1[1], point_2[1])),
|
||||
'z': (min(point_1[2], point_2[2]), max(point_1[2], point_2[2])), }
|
||||
|
||||
|
||||
class Sphere(Geometry3D):
|
||||
|
||||
def __init__(self, center, radius):
|
||||
x, y, z, v_1, v_2, u_1, u_2 = symbols('x y z v_1 v_2 u_1 u_2')
|
||||
ranges = {v_1: (0, 1), v_2: (0, 1), u_1: (0, 1), u_2: (0, 1)}
|
||||
r_1 = sqrt(-log(v_1)) * cos(2 * pi * u_1)
|
||||
r_2 = sqrt(-log(v_1)) * sin(2 * pi * u_1)
|
||||
r_3 = sqrt(-log(v_2)) * cos(2 * pi * u_2)
|
||||
|
||||
norm = sqrt(r_1 ** 2 + r_2 ** 2 + r_3 ** 2)
|
||||
edge_1 = Edge(functions={'x': center[0] + radius * r_1 / norm,
|
||||
'y': center[1] + radius * r_2 / norm,
|
||||
'z': center[2] + radius * r_3 / norm,
|
||||
'normal_x': r_1 / norm,
|
||||
'normal_y': r_2 / norm,
|
||||
'normal_z': r_3 / norm},
|
||||
ranges=ranges,
|
||||
area=4 * pi * radius ** 2)
|
||||
|
||||
self.edges = [edge_1]
|
||||
self.sdf = radius - sqrt((x - center[0]) ** 2 + (y - center[1]) ** 2 + (z - center[2]) ** 2)
|
||||
self.bounds = {'x': (center[0] - radius, center[0] + radius),
|
||||
'y': (center[1] - radius, center[1] + radius),
|
||||
'z': (center[2] - radius, center[2] + radius)}
|
||||
|
||||
|
||||
class Cylinder(Geometry3D):
|
||||
|
||||
def __init__(self, center, radius, height):
|
||||
x, y, z, h, r, theta = symbols('x y z h r theta')
|
||||
ranges = {h: (-1, 1), r: (0, 1), theta: (0, 2 * pi)}
|
||||
edge_1 = Edge(functions={'x': center[0] + radius * cos(theta),
|
||||
'y': center[1] + radius * sin(theta),
|
||||
'z': center[2] + 0.5 * h * height,
|
||||
'normal_x': 1 * cos(theta),
|
||||
'normal_y': 1 * sin(theta),
|
||||
'normal_z': 0},
|
||||
ranges=ranges,
|
||||
area=height * 2 * pi * radius)
|
||||
edge_2 = Edge(functions={'x': center[0] + sqrt(r) * radius * cos(theta),
|
||||
'y': center[1] + sqrt(r) * radius * sin(theta),
|
||||
'z': center[2] + 0.5 * height,
|
||||
'normal_x': 0,
|
||||
'normal_y': 0,
|
||||
'normal_z': 1},
|
||||
ranges=ranges,
|
||||
area=math.pi * radius ** 2)
|
||||
edge_3 = Edge(functions={'x': center[0] + sqrt(r) * radius * cos(theta),
|
||||
'y': center[1] + sqrt(r) * radius * sin(theta),
|
||||
'z': center[2] - 0.5 * height,
|
||||
'normal_x': 0,
|
||||
'normal_y': 0,
|
||||
'normal_z': -1},
|
||||
ranges=ranges,
|
||||
area=pi * radius ** 2)
|
||||
self.edges = [edge_1, edge_2, edge_3]
|
||||
|
||||
r_dist = sqrt((x - center[0]) ** 2 + (y - center[1]) ** 2)
|
||||
z_dist = Abs(z - center[2])
|
||||
outside_distance = sqrt(Min(0, radius - r_dist) ** 2 + Min(0, 0.5 * height - z_dist) ** 2)
|
||||
inside_distance = -1 * Min(Abs(Min(0, r_dist - radius)), Abs(Min(0, z_dist - 0.5 * height)))
|
||||
self.sdf = - (outside_distance + inside_distance)
|
||||
|
||||
self.bounds = {'x': (center[0] - radius, center[0] + radius),
|
||||
'y': (center[1] - radius, center[1] + radius),
|
||||
'z': (center[2] - height / 2, center[2] + height / 2)}
|
||||
|
|
@ -0,0 +1,170 @@
|
|||
"""Convert sympy expression to np functions
|
||||
todo: converges to torch_util
|
||||
|
||||
"""
|
||||
|
||||
import numpy as np
|
||||
from sympy import lambdify
|
||||
from typing import Iterable
|
||||
from functools import reduce
|
||||
import collections
|
||||
from sympy import Max, Min, Mul
|
||||
|
||||
__all__ = ['lambdify_np']
|
||||
|
||||
|
||||
class WrapSympy:
|
||||
is_sympy = True
|
||||
|
||||
@staticmethod
|
||||
def _wrapper_guide(args):
|
||||
func_1 = args[0]
|
||||
func_2 = args[1]
|
||||
cond_1 = (isinstance(func_1, WrapSympy) and not func_1.is_sympy)
|
||||
cond_2 = isinstance(func_2, WrapSympy) and not func_2.is_sympy
|
||||
cond_3 = (not isinstance(func_1, WrapSympy)) and isinstance(func_1, collections.Callable)
|
||||
cond_4 = (not isinstance(func_2, WrapSympy)) and isinstance(func_2, collections.Callable)
|
||||
return cond_1 or cond_2 or cond_3 or cond_4, func_1, func_2
|
||||
|
||||
|
||||
class WrapMax(Max, WrapSympy):
|
||||
def __new__(cls, *args, **kwargs):
|
||||
cond, func_1, func_2 = WrapMax._wrapper_guide(args)
|
||||
if cond:
|
||||
a = object.__new__(cls)
|
||||
a.f = func_1
|
||||
a.g = func_2
|
||||
a.is_sympy = False
|
||||
else:
|
||||
a = Max.__new__(cls, *args, **kwargs)
|
||||
if isinstance(a, WrapSympy):
|
||||
a.is_sympy = True
|
||||
return a
|
||||
|
||||
def __call__(self, **x):
|
||||
if not self.is_sympy:
|
||||
f = lambdify_np(self.f, x.keys())
|
||||
g = lambdify_np(self.g, x.keys())
|
||||
return np.maximum(f(**x), g(**x))
|
||||
else:
|
||||
f = lambdify_np(self, x.keys())
|
||||
return f(**x)
|
||||
|
||||
|
||||
class WrapMul(Mul, WrapSympy):
|
||||
def __new__(cls, *args, **kwargs):
|
||||
cond, func_1, func_2 = WrapMul._wrapper_guide(args)
|
||||
if cond:
|
||||
a = object.__new__(cls)
|
||||
a.f = func_1
|
||||
a.g = func_2
|
||||
a.is_sympy = False
|
||||
else:
|
||||
a = Mul.__new__(cls, *args, **kwargs)
|
||||
if isinstance(a, WrapSympy):
|
||||
a.is_sympy = True
|
||||
return a
|
||||
|
||||
def __call__(self, **x):
|
||||
if not self.is_sympy:
|
||||
f = lambdify_np(self.f, x.keys())
|
||||
g = lambdify_np(self.g, x.keys())
|
||||
return f(**x) * g(**x)
|
||||
else:
|
||||
f = lambdify_np(self, x.keys())
|
||||
return f(**x)
|
||||
|
||||
|
||||
class WrapMin(Min, WrapSympy):
|
||||
def __new__(cls, *args, **kwargs):
|
||||
cond, func_1, func_2 = WrapMin._wrapper_guide(args)
|
||||
if cond:
|
||||
a = object.__new__(cls)
|
||||
a.f = func_1
|
||||
a.g = func_2
|
||||
a.is_sympy = False
|
||||
else:
|
||||
a = Min.__new__(cls, *args, **kwargs)
|
||||
if isinstance(a, WrapSympy):
|
||||
a.is_sympy = True
|
||||
return a
|
||||
|
||||
def __call__(self, **x):
|
||||
if not self.is_sympy:
|
||||
f = lambdify_np(self.f, x.keys())
|
||||
g = lambdify_np(self.g, x.keys())
|
||||
return np.minimum(f(**x), g(**x))
|
||||
else:
|
||||
f = lambdify_np(self, x.keys())
|
||||
return f(**x)
|
||||
|
||||
|
||||
def _try_float(fn):
|
||||
try:
|
||||
fn = float(fn)
|
||||
except ValueError:
|
||||
pass
|
||||
except TypeError:
|
||||
pass
|
||||
return fn
|
||||
|
||||
|
||||
def _constant_bool(boolean: bool):
|
||||
def fn(**x):
|
||||
return np.ones_like(next(iter(x.items()))[1], dtype=bool) if boolean else np.zeros_like(
|
||||
next(iter(x.items()))[1], dtype=bool)
|
||||
|
||||
return fn
|
||||
|
||||
|
||||
def _constant_float(f):
|
||||
def fn(**x):
|
||||
return np.ones_like(next(iter(x.items()))[1]) * f
|
||||
|
||||
return fn
|
||||
|
||||
|
||||
def lambdify_np(f, r: Iterable):
|
||||
if isinstance(r, dict):
|
||||
r = r.keys()
|
||||
if isinstance(f, WrapSympy) and f.is_sympy:
|
||||
lambdify_f = lambdify([k for k in r], f, [PLACEHOLDER, 'numpy'])
|
||||
lambdify_f.input_keys = [k for k in r]
|
||||
return lambdify_f
|
||||
if isinstance(f, WrapSympy) and not f.is_sympy:
|
||||
return f
|
||||
if isinstance(f, collections.Callable):
|
||||
return f
|
||||
if isinstance(f, bool):
|
||||
return _constant_bool(f)
|
||||
f = _try_float(f)
|
||||
if isinstance(f, float):
|
||||
return _constant_float(f)
|
||||
else:
|
||||
lambdify_f = lambdify([k for k in r], f, [PLACEHOLDER, 'numpy'])
|
||||
lambdify_f.input_keys = [k for k in r]
|
||||
return lambdify_f
|
||||
|
||||
|
||||
PLACEHOLDER = {'amin': lambda x: reduce(lambda y, z: np.minimum(y, z), x),
|
||||
'amax': lambda x: reduce(lambda y, z: np.maximum(y, z), x),
|
||||
'Min': lambda *x: reduce(lambda y, z: np.minimum(y, z), x),
|
||||
'Max': lambda *x: reduce(lambda y, z: np.maximum(y, z), x),
|
||||
'Heaviside': lambda x: np.heaviside(x, 0),
|
||||
'equal': lambda x, y: np.isclose(x, y),
|
||||
'Xor': np.logical_xor,
|
||||
'cos': np.cos,
|
||||
'sin': np.sin,
|
||||
'tan': np.tan,
|
||||
'exp': np.exp,
|
||||
'sqrt': np.sqrt,
|
||||
'log': np.log,
|
||||
'sinh': np.sinh,
|
||||
'cosh': np.cosh,
|
||||
'tanh': np.tanh,
|
||||
'asin': np.arcsin,
|
||||
'acos': np.arccos,
|
||||
'atan': np.arctan,
|
||||
'Abs': np.abs,
|
||||
'DiracDelta': np.zeros_like,
|
||||
}
|
||||
|
|
@ -0,0 +1,200 @@
|
|||
"""Define Computational graph"""
|
||||
|
||||
import sympy as sp
|
||||
from typing import List, Dict, Union
|
||||
from copy import copy
|
||||
from collections import defaultdict
|
||||
import networkx as nx
|
||||
import matplotlib.pyplot as plt
|
||||
import math
|
||||
from idrlnet.variable import Variables
|
||||
from idrlnet.node import Node
|
||||
from idrlnet.header import logger, DIFF_SYMBOL
|
||||
from idrlnet.pde import PdeNode
|
||||
from idrlnet.net import NetNode
|
||||
|
||||
__all__ = ['ComputableNodeList', 'Vertex', 'VertexTaskPipeline']
|
||||
x, y = sp.symbols('x y')
|
||||
ComputableNodeList = [List[Union[PdeNode, NetNode]]]
|
||||
|
||||
|
||||
class Vertex(Node):
|
||||
counter = 0
|
||||
|
||||
def __init__(self, pre=None, next=None, node=None, ntype='c'):
|
||||
node = Node() if node is None else node
|
||||
self.__dict__ = node.__dict__.copy()
|
||||
self.index = type(self).counter
|
||||
type(self).counter += 1
|
||||
self.pre = pre if pre is not None else set()
|
||||
self.next = next if pre is not None else set()
|
||||
self.ntype = ntype
|
||||
assert self.ntype in ('d', 'c', 'r')
|
||||
|
||||
def __eq__(self, other):
|
||||
return self.index == other.index
|
||||
|
||||
def __hash__(self):
|
||||
return self.index
|
||||
|
||||
def __str__(self):
|
||||
info = f"index: {self.index}\n" + f"pre: {[node.index for node in self.pre]}\n" \
|
||||
+ f"next: {[node.index for node in self.next]}\n"
|
||||
return super().__str__() + info
|
||||
|
||||
|
||||
class VertexTaskPipeline:
|
||||
MAX_STACK_ALLOWED = 100000
|
||||
|
||||
@property
|
||||
def evaluation_order_list(self):
|
||||
return self._evaluation_order_list
|
||||
|
||||
@evaluation_order_list.setter
|
||||
def evaluation_order_list(self, evaluation_order_list):
|
||||
self._evaluation_order_list = evaluation_order_list
|
||||
|
||||
def __init__(self, nodes: ComputableNodeList, invar: Variables, req_names: List[str]):
|
||||
self.nodes = nodes
|
||||
self.req_names = req_names
|
||||
self.computable = set(invar.keys())
|
||||
|
||||
graph_nodes = set(Vertex(node=node) for node in nodes)
|
||||
req_name_dict: Dict[str, List[Vertex]] = defaultdict(list)
|
||||
|
||||
self.G = nx.DiGraph()
|
||||
self.egde_data = defaultdict(set)
|
||||
required_stack = []
|
||||
for req_name in req_names:
|
||||
final_graph_node = Vertex()
|
||||
if DIFF_SYMBOL in req_name:
|
||||
final_graph_node.derivatives = (req_name,)
|
||||
final_graph_node.inputs = tuple()
|
||||
else:
|
||||
final_graph_node.inputs = [req_name]
|
||||
final_graph_node.derivatives = tuple()
|
||||
final_graph_node.outputs = tuple()
|
||||
final_graph_node.name = f'<{req_name}>'
|
||||
final_graph_node.ntype = 'r'
|
||||
graph_nodes.add(final_graph_node)
|
||||
req_name_dict[req_name].append(final_graph_node)
|
||||
required_stack.append(final_graph_node)
|
||||
final_graph_node.evaluate = lambda x: x
|
||||
|
||||
logger.info('Constructing computation graph...')
|
||||
while len(req_name_dict) > 0:
|
||||
to_be_removed = set()
|
||||
to_be_added = defaultdict(list)
|
||||
if len(required_stack) >= self.MAX_STACK_ALLOWED:
|
||||
raise ValueError
|
||||
for req_name, current_gn in req_name_dict.items():
|
||||
req_name = tuple(req_name.split(DIFF_SYMBOL))
|
||||
match_score = -1
|
||||
match_gn = None
|
||||
for gn in graph_nodes:
|
||||
if gn in current_gn:
|
||||
continue
|
||||
for output in gn.outputs:
|
||||
output = tuple(output.split(DIFF_SYMBOL))
|
||||
if len(output) <= len(req_name) and req_name[:len(output)] == output and len(
|
||||
output) > match_score:
|
||||
match_score = len(output)
|
||||
match_gn = gn
|
||||
for p_in in invar.keys():
|
||||
p_in = tuple(p_in.split(DIFF_SYMBOL))
|
||||
if len(p_in) <= len(req_name) and req_name[:len(p_in)] == p_in and len(
|
||||
p_in) > match_score:
|
||||
match_score = len(p_in)
|
||||
match_gn = None
|
||||
for sub_gn in req_name_dict[DIFF_SYMBOL.join(req_name)]:
|
||||
self.G.add_edge(DIFF_SYMBOL.join(p_in), sub_gn.name)
|
||||
if match_score <= 0:
|
||||
raise Exception("Can't be computed: " + DIFF_SYMBOL.join(req_name))
|
||||
elif match_gn is not None:
|
||||
for sub_gn in req_name_dict[DIFF_SYMBOL.join(req_name)]:
|
||||
logger.info(f'{sub_gn.name}.{DIFF_SYMBOL.join(req_name)} <---- {match_gn.name}')
|
||||
match_gn.next.add(sub_gn)
|
||||
self.egde_data[(match_gn.name, sub_gn.name)].add(DIFF_SYMBOL.join(req_name))
|
||||
required_stack.append(match_gn)
|
||||
for sub_gn in req_name_dict[DIFF_SYMBOL.join(req_name)]:
|
||||
sub_gn.pre.add(match_gn)
|
||||
for p in match_gn.inputs:
|
||||
to_be_added[p].append(match_gn)
|
||||
for p in match_gn.derivatives:
|
||||
to_be_added[p].append(match_gn)
|
||||
for sub_gn in req_name_dict[DIFF_SYMBOL.join(req_name)]:
|
||||
self.G.add_edge(match_gn.name, sub_gn.name)
|
||||
to_be_removed.add(DIFF_SYMBOL.join(req_name))
|
||||
if len(to_be_removed) == 0 and len(req_name_dict) > 0:
|
||||
raise Exception("Can't be computed")
|
||||
for p in to_be_removed:
|
||||
req_name_dict.pop(p)
|
||||
self.computable.add(p)
|
||||
for k, v in to_be_added.items():
|
||||
if k in req_name_dict:
|
||||
req_name_dict[k].extend(v)
|
||||
else:
|
||||
req_name_dict[k] = v
|
||||
evaluation_order = []
|
||||
while len(required_stack) > 0:
|
||||
gn = required_stack.pop()
|
||||
if gn not in evaluation_order:
|
||||
evaluation_order.append(gn)
|
||||
self.computable = self.computable.union(set(gn.outputs))
|
||||
self.evaluation_order_list = evaluation_order
|
||||
self._graph_node_table = {node.name: node for node in graph_nodes}
|
||||
for key in invar:
|
||||
node = Vertex()
|
||||
node.name = key
|
||||
node.outputs = (key,)
|
||||
node.inputs = tuple()
|
||||
node.ntype = 'd'
|
||||
self._graph_node_table[key] = node
|
||||
logger.info('Computation graph constructed.')
|
||||
|
||||
def operation_order(self, invar: Variables):
|
||||
for node in self.evaluation_order_list:
|
||||
if not set(node.derivatives).issubset(invar.keys()):
|
||||
invar.differentiate_(independent_var=invar, required_derivatives=node.derivatives)
|
||||
invar.update(node.evaluate({**invar.subset(node.inputs), **invar.subset(node.derivatives)}))
|
||||
|
||||
def forward_pipeline(self, invar: Variables, req_names: List[str] = None) -> Variables:
|
||||
if req_names is None or set(req_names).issubset(set(self.computable)):
|
||||
outvar = copy(invar)
|
||||
self.operation_order(outvar)
|
||||
return outvar.subset(self.req_names if req_names is None else req_names)
|
||||
else:
|
||||
logger.info('The existing graph fails. Construct a temporary graph...')
|
||||
return VertexTaskPipeline(self.nodes, invar, req_names).forward_pipeline(invar)
|
||||
|
||||
def to_json(self):
|
||||
pass
|
||||
|
||||
def display(self, filename: str = None):
|
||||
_, ax = plt.subplots(1, 1, figsize=(8, 8))
|
||||
ax.axis('off')
|
||||
pos = nx.spring_layout(self.G, k=10 / (math.sqrt(self.G.order()) + 0.1))
|
||||
nx.draw_networkx_nodes(self.G, pos,
|
||||
nodelist=list(
|
||||
node for node in self.G.nodes if self._graph_node_table[node].ntype == 'c'),
|
||||
cmap=plt.get_cmap('jet'),
|
||||
node_size=1300, node_color="pink", alpha=0.5)
|
||||
nx.draw_networkx_nodes(self.G, pos,
|
||||
nodelist=list(
|
||||
node for node in self.G.nodes if self._graph_node_table[node].ntype == 'r'),
|
||||
cmap=plt.get_cmap('jet'),
|
||||
node_size=1300, node_color="green", alpha=0.3)
|
||||
nx.draw_networkx_nodes(self.G, pos,
|
||||
nodelist=list(
|
||||
node for node in self.G.nodes if self._graph_node_table[node].ntype == 'd'),
|
||||
cmap=plt.get_cmap('jet'),
|
||||
node_size=1300, node_color="blue", alpha=0.3)
|
||||
nx.draw_networkx_edges(self.G, pos, edge_color='r', arrows=True, arrowsize=30, arrowstyle="-|>")
|
||||
nx.draw_networkx_labels(self.G, pos)
|
||||
nx.draw_networkx_edge_labels(self.G, pos, edge_labels={k: ", ".join(v) for k, v in self.egde_data.items()},
|
||||
font_size=10)
|
||||
if filename is None:
|
||||
plt.show()
|
||||
else:
|
||||
plt.savefig(filename)
|
||||
plt.close()
|
||||
|
|
@ -0,0 +1,42 @@
|
|||
"""Initialize public objects"""
|
||||
|
||||
import logging
|
||||
import functools
|
||||
|
||||
DIFF_SYMBOL = "__"
|
||||
|
||||
|
||||
class TestFun:
|
||||
registered = []
|
||||
|
||||
def __init__(self, fun):
|
||||
self.fun = fun
|
||||
self.registered.append(self)
|
||||
|
||||
def __call__(self, *args, **kwargs):
|
||||
print(str(self.fun.__name__).center(50, '*'))
|
||||
self.fun()
|
||||
|
||||
@staticmethod
|
||||
def run():
|
||||
for fun in TestFun.registered:
|
||||
fun()
|
||||
|
||||
|
||||
def testmemo(fun):
|
||||
@functools.wraps(fun)
|
||||
def wrapper(*args, **kwargs):
|
||||
if id(fun) not in testmemo.memo:
|
||||
logger.info(f"'{fun}' needs tests")
|
||||
testmemo.memo.add(id(fun))
|
||||
fun(*args, **kwargs)
|
||||
|
||||
return wrapper
|
||||
|
||||
|
||||
testmemo.memo = set()
|
||||
|
||||
log_format = '[%(asctime)s] [%(levelname)s] %(message)s'
|
||||
handlers = [logging.FileHandler('train.log', mode='a'), logging.StreamHandler()]
|
||||
logging.basicConfig(format=log_format, level=logging.INFO, datefmt='%d-%b-%y %H:%M:%S', handlers=handlers)
|
||||
logger = logging.getLogger(__name__)
|
||||
|
|
@ -0,0 +1,93 @@
|
|||
"""Define NetNode"""
|
||||
import torch
|
||||
from idrlnet.node import Node
|
||||
from typing import Tuple, List, Dict, Union
|
||||
from contextlib import ExitStack
|
||||
|
||||
__all__ = ['NetNode']
|
||||
|
||||
|
||||
class WrapEvaluate:
|
||||
def __init__(self, binding_node: 'NetNode'):
|
||||
self.binding_node = binding_node
|
||||
|
||||
def __call__(self, inputs):
|
||||
keep_type = None
|
||||
if isinstance(inputs, dict):
|
||||
keep_type = dict
|
||||
inputs = torch.cat(
|
||||
[torch.tensor(inputs[key], dtype=torch.float32) if not isinstance(inputs[key], torch.Tensor) else
|
||||
inputs[
|
||||
key] for key in inputs], dim=1)
|
||||
with ExitStack() as es:
|
||||
if self.binding_node.require_no_grad:
|
||||
es.enter_context(torch.no_grad())
|
||||
output_var = self.binding_node.net(inputs)
|
||||
if keep_type == dict:
|
||||
output_var = {outkey: output_var[:, i:i + 1] for i, outkey in enumerate(self.binding_node.outputs)}
|
||||
return output_var
|
||||
|
||||
|
||||
class NetNode(Node):
|
||||
counter = 0
|
||||
|
||||
@property
|
||||
def fixed(self):
|
||||
return self._fixed
|
||||
|
||||
@fixed.setter
|
||||
def fixed(self, fixed: bool):
|
||||
self._fixed = fixed
|
||||
|
||||
@property
|
||||
def require_no_grad(self):
|
||||
return self._require_no_grad
|
||||
|
||||
@require_no_grad.setter
|
||||
def require_no_grad(self, require_no_grad: bool):
|
||||
self._require_no_grad = require_no_grad
|
||||
|
||||
@property
|
||||
def is_reference(self):
|
||||
return self._is_reference
|
||||
|
||||
@is_reference.setter
|
||||
def is_reference(self, is_reference: bool):
|
||||
self._is_reference = is_reference
|
||||
|
||||
@property
|
||||
def net(self):
|
||||
return self._net
|
||||
|
||||
@net.setter
|
||||
def net(self, net):
|
||||
self._net = net
|
||||
|
||||
def __init__(self, inputs: Union[Tuple, List[str]], outputs: Union[Tuple, List[str]],
|
||||
net: torch.nn.Module, fixed: bool = False, require_no_grad: bool = False, is_reference=False,
|
||||
name=None, *args, **kwargs):
|
||||
self.is_reference = is_reference
|
||||
self.inputs: Union[Tuple, List[str]] = inputs
|
||||
self.outputs: Union[Tuple, List[str]] = outputs
|
||||
self.derivatives: Union[Tuple, List[str]] = []
|
||||
self.net: torch.nn.Module = net
|
||||
self.require_no_grad = require_no_grad
|
||||
self.fixed = fixed
|
||||
if name is not None:
|
||||
self.name = name
|
||||
else:
|
||||
# todo: make sure this is working
|
||||
self.name: str = "net_{}".format(type(self).counter)
|
||||
type(self).counter += 1
|
||||
self.evaluate = WrapEvaluate(binding_node=self)
|
||||
|
||||
def __str__(self):
|
||||
basic_info = super().__str__()
|
||||
|
||||
return basic_info + str(self.net)
|
||||
|
||||
def load_state_dict(self, state_dict: Dict[str, torch.Tensor], strict: bool = True):
|
||||
return self.net.load_state_dict(state_dict, strict)
|
||||
|
||||
def state_dict(self, destination=None, prefix: str = '', keep_vars: bool = False):
|
||||
return self.net.state_dict(destination, prefix, keep_vars)
|
||||
|
|
@ -0,0 +1,99 @@
|
|||
"""Define Basic Node"""
|
||||
from typing import Callable, List
|
||||
|
||||
from idrlnet.torch_util import torch_lambdify
|
||||
from idrlnet.variable import Variables
|
||||
from idrlnet.header import DIFF_SYMBOL
|
||||
|
||||
__all__ = ['Node']
|
||||
|
||||
|
||||
class Node(object):
|
||||
@property
|
||||
def inputs(self) -> List[str]:
|
||||
try:
|
||||
return self._inputs
|
||||
except:
|
||||
self._inputs = tuple()
|
||||
return self._inputs
|
||||
|
||||
@inputs.setter
|
||||
def inputs(self, inputs: List[str]):
|
||||
self._inputs = inputs
|
||||
|
||||
@property
|
||||
def outputs(self) -> List[str]:
|
||||
try:
|
||||
return self._outputs
|
||||
except:
|
||||
self._outputs = tuple()
|
||||
return self._outputs
|
||||
|
||||
@outputs.setter
|
||||
def outputs(self, outputs: List[str]):
|
||||
self._outputs = outputs
|
||||
|
||||
@property
|
||||
def derivatives(self) -> List[str]:
|
||||
try:
|
||||
return self._derivatives
|
||||
except:
|
||||
self._derivatives = []
|
||||
return self._derivatives
|
||||
|
||||
@derivatives.setter
|
||||
def derivatives(self, derivatives: List[str]):
|
||||
self._derivatives = derivatives
|
||||
|
||||
@property
|
||||
def evaluate(self) -> Callable:
|
||||
return self._evaluate
|
||||
|
||||
@evaluate.setter
|
||||
def evaluate(self, evaluate: Callable):
|
||||
self._evaluate = evaluate
|
||||
|
||||
@property
|
||||
def name(self) -> str:
|
||||
try:
|
||||
return self._name
|
||||
except:
|
||||
self._name = 'Node' + str(id(self))
|
||||
return self._name
|
||||
|
||||
@name.setter
|
||||
def name(self, name: str):
|
||||
self._name = name
|
||||
|
||||
@classmethod
|
||||
def new_node(cls, name: str = None, tf_eq: Callable = None, free_symbols: List[str] = None, *args,
|
||||
**kwargs) -> 'Node':
|
||||
node = cls()
|
||||
node.evaluate = LambdaTorchFun(free_symbols, tf_eq, name)
|
||||
node.inputs = [x for x in free_symbols if DIFF_SYMBOL not in x]
|
||||
node.derivatives = [x for x in free_symbols if DIFF_SYMBOL in x]
|
||||
node.outputs = [name, ]
|
||||
node.name = name
|
||||
return node
|
||||
|
||||
def __str__(self):
|
||||
str_list = ["Basic properties:\n",
|
||||
"name: {}\n".format(self.name),
|
||||
"inputs: {}\n".format(self.inputs),
|
||||
"derivatives: {}\n".format(self.derivatives),
|
||||
"outputs: {}\n".format(self.outputs), ]
|
||||
return ''.join(str_list)
|
||||
|
||||
|
||||
class LambdaTorchFun:
|
||||
def __init__(self, free_symbols, tf_eq, name):
|
||||
self.lambda_tf_eq = torch_lambdify(free_symbols, tf_eq)
|
||||
self.tf_eq = tf_eq
|
||||
self.name = name
|
||||
self.free_symbols = free_symbols
|
||||
|
||||
def __call__(self, var: Variables):
|
||||
new_var = {}
|
||||
for key, values in var.items():
|
||||
new_var[key] = values
|
||||
return {self.name: self.lambda_tf_eq(**new_var)}
|
||||
|
|
@ -0,0 +1,82 @@
|
|||
"""Define Optimizers and LR schedulers"""
|
||||
|
||||
import abc
|
||||
import torch
|
||||
import inspect
|
||||
import math
|
||||
from typing import Dict
|
||||
|
||||
__all__ = ['get_available_class', 'Optimizable']
|
||||
|
||||
|
||||
def get_available_class(module, class_name) -> Dict[str, type]:
|
||||
"""Search specified subclasses of the given class in module.
|
||||
|
||||
:param module: The module name
|
||||
:type module: module
|
||||
:param class_name: the parent class
|
||||
:type class_name: type
|
||||
:return: A dict mapping from subclass.name to subclass
|
||||
:rtype: Dict[str, type]
|
||||
"""
|
||||
return dict(filter(
|
||||
lambda x: inspect.isclass(x[1])
|
||||
and issubclass(x[1], class_name)
|
||||
and (not x[1] == class_name),
|
||||
inspect.getmembers(module)))
|
||||
|
||||
|
||||
class Optimizable(metaclass=abc.ABCMeta):
|
||||
"""An abstract class for organizing optimization related configuration and operations.
|
||||
The interface is implemented by solver.Solver
|
||||
"""
|
||||
OPTIMIZER_MAP = get_available_class(module=torch.optim, class_name=torch.optim.Optimizer)
|
||||
SCHEDULE_MAP = get_available_class(module=torch.optim.lr_scheduler,
|
||||
class_name=torch.optim.lr_scheduler._LRScheduler)
|
||||
|
||||
@property
|
||||
def optimizers(self):
|
||||
return self._optimizers
|
||||
|
||||
@optimizers.setter
|
||||
def optimizers(self, optimizers):
|
||||
self._optimizers = optimizers
|
||||
|
||||
@property
|
||||
def schedulers(self):
|
||||
return self._schedulers
|
||||
|
||||
@schedulers.setter
|
||||
def schedulers(self, schedulers):
|
||||
self._schedulers = schedulers
|
||||
|
||||
@abc.abstractmethod
|
||||
def configure_optimizers(self):
|
||||
raise NotImplementedError
|
||||
|
||||
def parse_configure(self, **kwargs):
|
||||
self.parse_optimizer(**kwargs)
|
||||
self.parse_lr_schedule(**kwargs)
|
||||
self.configure_optimizers()
|
||||
|
||||
def parse_optimizer(self, **kwargs):
|
||||
default_config = dict(optimizer='Adam', lr=1e-3)
|
||||
default_config.update(kwargs.get('opt_config', {}))
|
||||
self.optimizer_config = default_config
|
||||
|
||||
def parse_lr_schedule(self, **kwargs):
|
||||
default_config = dict(scheduler='ExponentialLR', gamma=math.pow(0.95, 0.001), last_epoch=-1)
|
||||
default_config.update(kwargs.get('schedule_config', {}))
|
||||
self.schedule_config = default_config
|
||||
|
||||
def __str__(self):
|
||||
if 'optimizer_config' in self.__dict__:
|
||||
opt_str = str(self.optimizer_config)
|
||||
else:
|
||||
opt_str = str('optimizer is empty...')
|
||||
|
||||
if 'schedule_config' in self.__dict__:
|
||||
schedule_str = str(self.schedule_config)
|
||||
else:
|
||||
schedule_str = str('scheduler is empty...')
|
||||
return "\n".join([opt_str, schedule_str])
|
||||
|
|
@ -0,0 +1,91 @@
|
|||
"""Define PdeNode"""
|
||||
|
||||
from typing import List, Dict
|
||||
from idrlnet.node import Node
|
||||
from idrlnet.torch_util import _replace_derivatives
|
||||
from idrlnet.header import DIFF_SYMBOL
|
||||
from idrlnet.variable import Variables
|
||||
|
||||
__all__ = ['PdeNode', 'ExpressionNode']
|
||||
|
||||
|
||||
class PdeEvaluate:
|
||||
"""A wrapper for PdeNode.evaluate"""
|
||||
|
||||
def __init__(self, binding_pde):
|
||||
self.binding_pde = binding_pde
|
||||
|
||||
def __call__(self, inputs: Variables) -> Variables:
|
||||
result = Variables()
|
||||
for node in self.binding_pde.sub_nodes:
|
||||
sub_inputs = {k: v for k, v in Variables(inputs).items() if
|
||||
k in node.inputs or k in node.derivatives}
|
||||
r = node.evaluate(sub_inputs)
|
||||
result.update(r)
|
||||
return result
|
||||
|
||||
|
||||
class PdeNode(Node):
|
||||
@property
|
||||
def suffix(self) -> str:
|
||||
return self._suffix
|
||||
|
||||
@suffix.setter
|
||||
def suffix(self, suffix: str):
|
||||
# todo: check suffix
|
||||
self._suffix = suffix
|
||||
|
||||
@property
|
||||
def equations(self) -> Dict:
|
||||
return self._equations
|
||||
|
||||
@equations.setter
|
||||
def equations(self, equations: Dict):
|
||||
self._equations = equations
|
||||
|
||||
@property
|
||||
def sub_nodes(self) -> List:
|
||||
return self._sub_nodes
|
||||
|
||||
@sub_nodes.setter
|
||||
def sub_nodes(self, sub_nodes: List):
|
||||
self._sub_nodes = sub_nodes
|
||||
|
||||
def __init__(self, suffix: str = "", **kwargs):
|
||||
if len(suffix) > 0:
|
||||
self.suffix = '[' + kwargs['suffix'] + ']' # todo: check prefix
|
||||
else:
|
||||
self.suffix = ''
|
||||
self.name = type(self).__name__ + self.suffix
|
||||
self.evaluate = PdeEvaluate(self)
|
||||
|
||||
def make_nodes(self) -> None:
|
||||
self.sub_nodes = []
|
||||
free_symbols_set = set()
|
||||
name_set = set()
|
||||
for name, eq in self.equations.items():
|
||||
torch_eq = _replace_derivatives(eq)
|
||||
free_symbols = [x.name for x in torch_eq.free_symbols]
|
||||
free_symbols_set.update(set(free_symbols))
|
||||
name = name + self.suffix
|
||||
node = Node.new_node(name, torch_eq, free_symbols)
|
||||
name_set.update({name})
|
||||
self.sub_nodes.append(node)
|
||||
self.inputs = [x for x in free_symbols_set if DIFF_SYMBOL not in x]
|
||||
self.derivatives = [x for x in free_symbols_set if DIFF_SYMBOL in x]
|
||||
self.outputs = [x for x in name_set]
|
||||
|
||||
def __str__(self):
|
||||
subnode_str = "\n\n".join(
|
||||
str(sub_node) + "Equation: \n" + str(self.equations[sub_node.name]) for sub_node in self.sub_nodes)
|
||||
return super().__str__() + "subnodes".center(30, '-') + '\n' + subnode_str
|
||||
|
||||
|
||||
# todo: test required
|
||||
class ExpressionNode(PdeNode):
|
||||
def __init__(self, expression, name, **kwargs):
|
||||
super().__init__(**kwargs)
|
||||
self.equations = dict()
|
||||
self.equations[name] = expression
|
||||
self.name = name
|
||||
self.make_nodes()
|
||||
|
|
@ -0,0 +1,2 @@
|
|||
from .equations import *
|
||||
from .operator import *
|
||||
|
|
@ -0,0 +1,152 @@
|
|||
"""Predefined equations
|
||||
|
||||
"""
|
||||
from sympy import Function, Number, symbols
|
||||
|
||||
from idrlnet.pde import PdeNode
|
||||
|
||||
__all__ = ['DiffusionNode', 'NavierStokesNode', 'WaveNode', 'BurgersNode', 'SchrodingerNode', 'AllenCahnNode']
|
||||
|
||||
|
||||
def symbolize(s, input_variables=None):
|
||||
if type(s) in (list, tuple):
|
||||
return [symbolize(_s) for _s in s]
|
||||
elif type(s) is str:
|
||||
s = Function(s)(*input_variables)
|
||||
elif type(s) in [float, int]:
|
||||
s = Number(s)
|
||||
return s
|
||||
|
||||
|
||||
class DiffusionNode(PdeNode):
|
||||
def __init__(self, T='T', D='D', Q=0, dim=3, time=True, **kwargs):
|
||||
super().__init__(**kwargs)
|
||||
self.T = T
|
||||
x, y, z, t = symbols('x y z t')
|
||||
input_variables = {'x': x, 'y': y, 'z': z, 't': t}
|
||||
assert type(T) == str, "T should be string"
|
||||
|
||||
T = symbolize(T, input_variables=input_variables)
|
||||
D = symbolize(D, input_variables=input_variables)
|
||||
Q = symbolize(Q, input_variables=input_variables)
|
||||
|
||||
self.equations = {'diffusion_' + self.T: -Q}
|
||||
if time:
|
||||
self.equations['diffusion_' + self.T] += T.diff(t)
|
||||
coord = [x, y, z]
|
||||
for i in range(dim):
|
||||
s = coord[i]
|
||||
self.equations['diffusion_' + self.T] -= (D * T.diff(s)).diff(s)
|
||||
self.make_nodes()
|
||||
|
||||
|
||||
class NavierStokesNode(PdeNode):
|
||||
def __init__(self, nu=0.1, rho=1., dim=2., time=False, **kwargs):
|
||||
super().__init__(**kwargs)
|
||||
self.dim = dim
|
||||
assert self.dim in [2, 3], "dim should be 2 or 3"
|
||||
self.time = time
|
||||
x, y, z, t = symbols('x y z t')
|
||||
input_variables = {'x': x, 'y': y, 'z': z, 't': t}
|
||||
if self.dim == 2:
|
||||
input_variables.pop('z')
|
||||
if not self.time:
|
||||
input_variables.pop('t')
|
||||
|
||||
u = symbolize('u', input_variables)
|
||||
v = symbolize('v', input_variables)
|
||||
w = symbolize('w', input_variables) if self.dim == 3 else Number(0)
|
||||
p = symbolize('p', input_variables)
|
||||
nu = symbolize(nu, input_variables)
|
||||
rho = symbolize(rho, input_variables)
|
||||
mu = rho * nu
|
||||
self.equations = {'continuity': rho.diff(t) + (rho * u).diff(x) + (rho * v).diff(y) + (rho * w).diff(z),
|
||||
'momentum_x': ((rho * u).diff(t)
|
||||
+ (u * ((rho * u).diff(x)) + v * ((rho * u).diff(y)) + w * ((rho * u).diff(z)))
|
||||
+ p.diff(x)
|
||||
- (mu * u.diff(x)).diff(x)
|
||||
- (mu * u.diff(y)).diff(y)
|
||||
- (mu * u.diff(z)).diff(z)),
|
||||
'momentum_y': ((rho * v).diff(t)
|
||||
+ (u * ((rho * v).diff(x)) + v * ((rho * v).diff(y)) + w * ((rho * v).diff(z)))
|
||||
+ p.diff(y)
|
||||
- (mu * v.diff(x)).diff(x)
|
||||
- (mu * v.diff(y)).diff(y)
|
||||
- (mu * v.diff(z)).diff(z)), }
|
||||
|
||||
if self.dim == 3:
|
||||
self.equations['momentum_z'] = ((rho * w).diff(t)
|
||||
+ (u * ((rho * w).diff(x)) + v * ((rho * w).diff(y)) + w * (
|
||||
(rho * w).diff(z))) + p.diff(z) - (mu * w.diff(x)).diff(x) - (mu * w.diff(y)).diff(y) - (
|
||||
mu * w.diff(z)).diff(z))
|
||||
self.make_nodes()
|
||||
|
||||
|
||||
class WaveNode(PdeNode):
|
||||
def __init__(self, u='u', c='c', dim=3, time=True, **kwargs):
|
||||
super().__init__(**kwargs)
|
||||
self.u = u
|
||||
self.dim = dim
|
||||
self.time = time
|
||||
x, y, z, t = symbols('x y z t')
|
||||
input_variables = {'x': x, 'y': y, 'z': z, 't': t}
|
||||
assert self.dim in [1, 2, 3], "dim should be 1, 2 or 3."
|
||||
if self.dim == 1:
|
||||
input_variables.pop('y')
|
||||
input_variables.pop('z')
|
||||
elif self.dim == 2:
|
||||
input_variables.pop('z')
|
||||
if not self.time:
|
||||
input_variables.pop('t')
|
||||
assert type(u) == str, "u should be string"
|
||||
u = symbolize(u, input_variables)
|
||||
c = symbolize(c, input_variables)
|
||||
self.equations = {'wave_equation': (u.diff(t, 2)
|
||||
- (c ** 2 * u.diff(x)).diff(x)
|
||||
- (c ** 2 * u.diff(y)).diff(y)
|
||||
- (c ** 2 * u.diff(z)).diff(z))}
|
||||
self.make_nodes()
|
||||
|
||||
|
||||
class BurgersNode(PdeNode):
|
||||
def __init__(self, u: str = 'u', v='v'):
|
||||
super().__init__()
|
||||
x, t = symbols('x t')
|
||||
input_variables = {'x': x, 't': t}
|
||||
|
||||
assert type(u) == str, "u needs to be string"
|
||||
u = symbolize(u, input_variables)
|
||||
v = symbolize(v, input_variables)
|
||||
|
||||
self.equations = {f'burgers_{str(u)}': (u.diff(t) + u * u.diff(x) - v * (u.diff(x)).diff(x))}
|
||||
self.make_nodes()
|
||||
|
||||
|
||||
class SchrodingerNode(PdeNode):
|
||||
def __init__(self, u='u', v='v', c=0.5):
|
||||
super().__init__()
|
||||
self.c = c
|
||||
x, t = symbols('x t')
|
||||
input_variables = {'x': x, 't': t}
|
||||
|
||||
assert type(u) == str, "u should be string"
|
||||
u = symbolize(u, input_variables)
|
||||
|
||||
assert type(v) == str, "v should be string"
|
||||
v = symbolize(v, input_variables)
|
||||
self.equations = {'real': u.diff(t) + self.c * v.diff(x, 2) + (u ** 2 + v ** 2) * v,
|
||||
'imaginary': v.diff(t) - self.c * u.diff(x, 2) - (u ** 2 + v ** 2) * u}
|
||||
self.make_nodes()
|
||||
|
||||
|
||||
class AllenCahnNode(PdeNode):
|
||||
def __init__(self, u='u', gamma_1=0.0001, gamma_2=5):
|
||||
super().__init__()
|
||||
self.gama_1 = gamma_1
|
||||
self.gama_2 = gamma_2
|
||||
x, t = symbols('x t')
|
||||
input_variables = {'x': x, 't': t}
|
||||
assert type(u) == str, "u should be string"
|
||||
u = symbolize(u, input_variables)
|
||||
self.equations = {'AllenCahn_' + str(u): u.diff(t) - self.gama_1 * u.diff(x, 2) - self.gama_2 * (u - u ** 3)}
|
||||
self.make_nodes()
|
||||
|
|
@ -0,0 +1,365 @@
|
|||
"""Operators in PDE
|
||||
|
||||
"""
|
||||
import numpy as np
|
||||
import sympy as sp
|
||||
import torch
|
||||
from idrlnet.node import Node
|
||||
from idrlnet.pde import PdeNode
|
||||
from sympy import Symbol, Function, symbols, Number
|
||||
from typing import Union, List
|
||||
from idrlnet.torch_util import integral, _replace_derivatives, torch_lambdify
|
||||
from idrlnet.variable import Variables
|
||||
|
||||
__all__ = ['NormalGradient', 'Difference', 'Derivative', 'Curl', 'Divergence', 'ICNode', 'Int1DNode', 'IntEq']
|
||||
|
||||
|
||||
class NormalGradient(PdeNode):
|
||||
def __init__(self, T: Union[str, Symbol, float, int], dim=3, time=True):
|
||||
super().__init__()
|
||||
self.T = T
|
||||
self.dim = dim
|
||||
self.time = time
|
||||
|
||||
x, y, z, normal_x, normal_y, normal_z, t = symbols('x y z normal_x normal_y normal_z t')
|
||||
|
||||
input_variables = {'x': x,
|
||||
'y': y,
|
||||
'z': z,
|
||||
't': t}
|
||||
if self.dim == 1:
|
||||
input_variables.pop('y')
|
||||
input_variables.pop('z')
|
||||
elif self.dim == 2:
|
||||
input_variables.pop('z')
|
||||
if not self.time:
|
||||
input_variables.pop('t')
|
||||
|
||||
T = Function(T)(*input_variables)
|
||||
|
||||
self.equations = {'normal_gradient_' + self.T: (normal_x * T.diff(x)
|
||||
+ normal_y * T.diff(y)
|
||||
+ normal_z * T.diff(z))}
|
||||
self.make_nodes()
|
||||
|
||||
|
||||
class Difference(PdeNode):
|
||||
def __init__(self, T: Union[str, Symbol, float, int], S: Union[str, Symbol, float, int], dim=3, time=True):
|
||||
super().__init__()
|
||||
self.T = T
|
||||
self.S = S
|
||||
self.dim = dim
|
||||
self.time = time
|
||||
x, y, z = symbols('x y z')
|
||||
t = Symbol('t')
|
||||
input_variables = {'x': x,
|
||||
'y': y,
|
||||
'z': z,
|
||||
't': t}
|
||||
if self.dim == 1:
|
||||
input_variables.pop('y')
|
||||
input_variables.pop('z')
|
||||
elif self.dim == 2:
|
||||
input_variables.pop('z')
|
||||
if not self.time:
|
||||
input_variables.pop('t')
|
||||
|
||||
# variables to set the gradients (example Temperature)
|
||||
T = Function(T)(*input_variables)
|
||||
S = Function(S)(*input_variables)
|
||||
|
||||
# set equations
|
||||
self.equations = {}
|
||||
self.equations['difference_' + self.T + '_' + self.S] = T - S
|
||||
self.make_nodes()
|
||||
|
||||
|
||||
class Derivative(PdeNode):
|
||||
def __init__(self, T: Union[str, Symbol, float, int], p: Union[str, Symbol], S: Union[str, Symbol, float, int] = 0.,
|
||||
dim=3, time=True):
|
||||
super().__init__()
|
||||
self.T = T
|
||||
self.S = S
|
||||
self.dim = dim
|
||||
self.time = time
|
||||
x, y, z = symbols('x y z')
|
||||
t = Symbol('t')
|
||||
|
||||
input_variables = {'x': x,
|
||||
'y': y,
|
||||
'z': z,
|
||||
't': t}
|
||||
if self.dim == 1:
|
||||
input_variables.pop('y')
|
||||
input_variables.pop('z')
|
||||
elif self.dim == 2:
|
||||
input_variables.pop('z')
|
||||
if not self.time:
|
||||
input_variables.pop('t')
|
||||
if type(S) is str:
|
||||
S = Function(S)(*input_variables)
|
||||
elif type(S) in [float, int]:
|
||||
S = Number(S)
|
||||
if isinstance(p, str):
|
||||
p = Symbol(p)
|
||||
T = Function(T)(*input_variables)
|
||||
self.equations = {}
|
||||
if isinstance(S, Function):
|
||||
self.equations['derivative_' + self.T + ':' + str(p) + '_' + str(self.S)] = T.diff(p) - S
|
||||
else:
|
||||
self.equations['derivative_' + self.T + ':' + str(p)] = T.diff(p) - S
|
||||
self.make_nodes()
|
||||
|
||||
|
||||
class Curl(PdeNode):
|
||||
def __init__(self, vector, curl_name=None):
|
||||
super().__init__()
|
||||
if curl_name is None:
|
||||
curl_name = ['u', 'v', 'w']
|
||||
x, y, z = symbols('x y z')
|
||||
input_variables = {'x': x, 'y': y, 'z': z}
|
||||
|
||||
v_0 = vector[0]
|
||||
v_1 = vector[1]
|
||||
v_2 = vector[2]
|
||||
if type(v_0) is str:
|
||||
v_0 = Function(v_0)(*input_variables)
|
||||
elif type(v_0) in [float, int]:
|
||||
v_0 = Number(v_0)
|
||||
if type(v_1) is str:
|
||||
v_1 = Function(v_1)(*input_variables)
|
||||
elif type(v_1) in [float, int]:
|
||||
v_1 = Number(v_1)
|
||||
if type(v_2) is str:
|
||||
v_2 = Function(v_2)(*input_variables)
|
||||
elif type(v_2) in [float, int]:
|
||||
v_2 = Number(v_2)
|
||||
|
||||
curl_0 = v_2.diff(y) - v_1.diff(z)
|
||||
curl_1 = v_0.diff(z) - v_2.diff(x)
|
||||
curl_2 = v_1.diff(x) - v_0.diff(y)
|
||||
|
||||
self.equations = {}
|
||||
self.equations[curl_name[0]] = curl_0
|
||||
self.equations[curl_name[1]] = curl_1
|
||||
self.equations[curl_name[2]] = curl_2
|
||||
|
||||
|
||||
class Divergence(PdeNode):
|
||||
def __init__(self, vector, div_name='div_v'):
|
||||
super().__init__()
|
||||
x, y, z = symbols('x y z')
|
||||
|
||||
input_variables = {'x': x, 'y': y, 'z': z}
|
||||
|
||||
v_0 = vector[0]
|
||||
v_1 = vector[1]
|
||||
v_2 = vector[2]
|
||||
|
||||
if type(v_0) is str:
|
||||
v_0 = Function(v_0)(*input_variables)
|
||||
elif type(v_0) in [float, int]:
|
||||
v_0 = Number(v_0)
|
||||
if type(v_1) is str:
|
||||
v_1 = Function(v_1)(*input_variables)
|
||||
elif type(v_1) in [float, int]:
|
||||
v_1 = Number(v_1)
|
||||
if type(v_2) is str:
|
||||
v_2 = Function(v_2)(*input_variables)
|
||||
elif type(v_2) in [float, int]:
|
||||
v_2 = Number(v_2)
|
||||
|
||||
self.equations = {}
|
||||
self.equations[div_name] = v_0 + v_1 + v_2
|
||||
|
||||
|
||||
class ICNode(PdeNode):
|
||||
def __init__(self, T: Union[str, Symbol, int, float, List[Union[str, Symbol, int, float]]], dim: int = 2,
|
||||
time: bool = False,
|
||||
reduce_name: str = None):
|
||||
super().__init__()
|
||||
if reduce_name is None:
|
||||
reduce_name = str(T)
|
||||
self.T = T
|
||||
self.dim = dim
|
||||
self.time = time
|
||||
self.reduce_name = reduce_name
|
||||
|
||||
x, y, z = symbols('x y z')
|
||||
normal_x = Symbol('normal_x')
|
||||
normal_y = Symbol('normal_y')
|
||||
normal_z = Symbol('normal_z')
|
||||
area = Symbol('area')
|
||||
|
||||
t = Symbol('t')
|
||||
|
||||
input_variables = {'x': x,
|
||||
'y': y,
|
||||
'z': z,
|
||||
't': t}
|
||||
if self.dim == 1:
|
||||
input_variables.pop('y')
|
||||
input_variables.pop('z')
|
||||
elif self.dim == 2:
|
||||
input_variables.pop('z')
|
||||
if not self.time:
|
||||
input_variables.pop('t')
|
||||
|
||||
def sympify_T(T: Union[str, Symbol, int, float, List[Union[str, Symbol, int, float]]]) -> Union[
|
||||
Symbol, List[Symbol]]:
|
||||
if isinstance(T, list):
|
||||
return [sympify_T(_T) for _T in T]
|
||||
elif type(T) is str:
|
||||
T = Function(T)(*input_variables)
|
||||
elif type(T) in [float, int]:
|
||||
T = Number(T)
|
||||
return T
|
||||
|
||||
T = sympify_T(T)
|
||||
# set equations
|
||||
self.equations = {}
|
||||
if isinstance(T, list):
|
||||
if self.dim == 3:
|
||||
self.equations['integral_' + self.reduce_name] = integral((normal_x * T[0]
|
||||
+ normal_y * T[1]
|
||||
+ normal_z * T[2]) * area)
|
||||
if self.dim == 2:
|
||||
self.equations['integral_' + self.reduce_name] = integral((normal_x * T[0]
|
||||
+ normal_y * T[1]) * area)
|
||||
else:
|
||||
self.equations['integral_' + self.reduce_name] = integral(T * area)
|
||||
self.make_nodes()
|
||||
|
||||
|
||||
class Int1DNode(PdeNode):
|
||||
counter = 0
|
||||
|
||||
def __init__(self, expression, expression_name, lb, ub, var: Union[str, sp.Symbol] = 's', degree=20, **kwargs):
|
||||
super().__init__(**kwargs)
|
||||
x = sp.Symbol('x')
|
||||
self.equations = {}
|
||||
self.var = sp.Symbol(var) if isinstance(var, str) else var
|
||||
self.degree = degree
|
||||
quad_s, quad_w = np.polynomial.legendre.leggauss(self.degree)
|
||||
self.quad_s = torch.tensor(quad_s, dtype=torch.float32)
|
||||
self.quad_w = torch.tensor(quad_w, dtype=torch.float32)
|
||||
|
||||
if type(lb) is str:
|
||||
self.lb = sp.Function(lb)(x)
|
||||
elif type(lb) in [float, int]:
|
||||
self.lb = sp.Number(lb)
|
||||
else:
|
||||
self.lb = lb
|
||||
|
||||
if type(ub) is str:
|
||||
self.ub = sp.Function(ub)(x)
|
||||
elif type(ub) in [float, int]:
|
||||
self.ub = sp.Number(ub)
|
||||
else:
|
||||
self.ub = ub
|
||||
|
||||
if type(expression) in [float, int]:
|
||||
self.equations[expression_name] = sp.Number(expression)
|
||||
elif isinstance(expression, sp.Expr):
|
||||
self.equations[expression_name] = expression
|
||||
else:
|
||||
raise
|
||||
|
||||
if 'funs' in kwargs.keys():
|
||||
self.funs = kwargs['funs']
|
||||
else:
|
||||
self.funs = {}
|
||||
self.computable_name = set(*[fun['output_map'].values() for _, fun in self.funs.items()])
|
||||
self.fun_require_input = set(
|
||||
*[set(fun['eval'].inputs) - set(fun['input_map'].keys()) for _, fun in self.funs.items()])
|
||||
|
||||
self.make_nodes()
|
||||
|
||||
def make_nodes(self) -> None:
|
||||
self.sub_nodes = []
|
||||
free_symbols_set = set()
|
||||
name_set = set()
|
||||
for name, eq in self.equations.items():
|
||||
self.lb = _replace_derivatives(self.lb)
|
||||
self.ub = _replace_derivatives(self.ub)
|
||||
eq = _replace_derivatives(eq)
|
||||
free_symbols_set.update(set(x.name for x in self.ub.free_symbols))
|
||||
free_symbols_set.update(set(x.name for x in self.lb.free_symbols))
|
||||
free_symbols_set.update(set(x.name for x in eq.free_symbols))
|
||||
for ele in self.fun_require_input:
|
||||
free_symbols_set.add(ele)
|
||||
if self.var.name in free_symbols_set:
|
||||
free_symbols_set.remove(self.var.name)
|
||||
|
||||
name = name + self.suffix
|
||||
node = self.new_node(name, eq, list(free_symbols_set))
|
||||
name_set.update({name})
|
||||
self.sub_nodes.append(node)
|
||||
|
||||
self.inputs = [x for x in free_symbols_set if x not in self.funs.keys()]
|
||||
self.derivatives = []
|
||||
self.outputs = [x for x in name_set]
|
||||
|
||||
def new_node(self, name: str = None, tf_eq: sp.Expr = None, free_symbols: List[str] = None, *args, **kwargs):
|
||||
out_symbols = [x for x in free_symbols if x not in self.funs.keys()]
|
||||
lb_lambda = torch_lambdify(out_symbols, self.lb)
|
||||
ub_lambda = torch_lambdify(out_symbols, self.ub)
|
||||
eq_lambda = torch_lambdify([*free_symbols, self.var.name], tf_eq)
|
||||
node = Node()
|
||||
node.evaluate = IntEq(self, lb_lambda, ub_lambda, out_symbols, free_symbols, eq_lambda, name)
|
||||
node.inputs = [x for x in free_symbols if x not in self.funs.keys()]
|
||||
node.derivatives = []
|
||||
node.outputs = [name]
|
||||
node.name = name
|
||||
return node
|
||||
|
||||
|
||||
class IntEq:
|
||||
def __init__(self, binding_node, lb_lambda, ub_lambda, out_symbols, free_symbols, eq_lambda, name):
|
||||
self.binding_node = binding_node
|
||||
self.lb_lambda = lb_lambda
|
||||
self.ub_lambda = ub_lambda
|
||||
self.out_symbols = out_symbols
|
||||
self.free_symbols = free_symbols
|
||||
self.eq_lambda = eq_lambda
|
||||
self.name = name
|
||||
|
||||
def __call__(self, var: Variables):
|
||||
var = {k: v for k, v in var.items()}
|
||||
lb_value = self.lb_lambda(**{k: v for k, v in var.items() if k in self.out_symbols})
|
||||
ub_value = self.ub_lambda(**{k: v for k, v in var.items() if k in self.out_symbols})
|
||||
|
||||
xx = dict()
|
||||
for syp in self.free_symbols:
|
||||
if syp not in var.keys():
|
||||
continue
|
||||
value = var[syp]
|
||||
_value = torch.ones_like(self.binding_node.quad_s) * value
|
||||
_value = _value.reshape(-1, 1)
|
||||
xx.update({syp: _value})
|
||||
|
||||
quad_w = (ub_value - lb_value) / 2 * self.binding_node.quad_w
|
||||
quad_s = (self.binding_node.quad_s + 1) * (ub_value - lb_value) / 2 + lb_value
|
||||
shape = quad_w.shape
|
||||
|
||||
quad_w = quad_w.reshape(-1, 1)
|
||||
quad_s = quad_s.reshape(-1, 1)
|
||||
|
||||
new_var = dict()
|
||||
for _, fun in self.binding_node.funs.items():
|
||||
input_map = fun['input_map']
|
||||
output_map = fun['output_map']
|
||||
tmp_var = dict()
|
||||
for k, v in xx.items():
|
||||
tmp_var[k] = v
|
||||
for k, v in input_map.items():
|
||||
tmp_var[k] = quad_s
|
||||
res = fun['eval'].evaluate(tmp_var)
|
||||
for k, v in output_map.items():
|
||||
res[v] = res.pop(k)
|
||||
new_var.update(res)
|
||||
xx.update(new_var)
|
||||
|
||||
values = quad_w * self.eq_lambda(**dict(**{self.binding_node.var.name: quad_s}, **xx))
|
||||
values = values.reshape(shape)
|
||||
return {self.name: values.sum(1, keepdim=True)}
|
||||
|
|
@ -0,0 +1,40 @@
|
|||
"""Concrete predefined callbacks"""
|
||||
|
||||
import abc
|
||||
from enum import Enum
|
||||
from typing import Dict, List
|
||||
|
||||
|
||||
class Signal(Enum):
|
||||
REGISTER = 'signal_register'
|
||||
SOLVE_START = 'signal_solve_start'
|
||||
TRAIN_PIPE_START = 'signal_train_pipe_start'
|
||||
BEFORE_COMPUTE_LOSS = 'before_compute_loss'
|
||||
AFTER_COMPUTE_LOSS = 'compute_loss'
|
||||
BEFORE_BACKWARD = 'signal_before_backward'
|
||||
TRAIN_PIPE_END = 'signal_train_pipe_end'
|
||||
SOLVE_END = 'signal_solve_end'
|
||||
|
||||
|
||||
class Receiver(metaclass=abc.ABCMeta):
|
||||
@abc.abstractmethod
|
||||
def receive_notify(self, obj: object, message: Dict):
|
||||
raise NotImplementedError('Method receive_notify() not implemented!')
|
||||
|
||||
|
||||
class Notifier:
|
||||
@property
|
||||
def receivers(self):
|
||||
return self._receivers
|
||||
|
||||
@receivers.setter
|
||||
def receivers(self, receivers: List[Receiver]):
|
||||
self._receivers = receivers
|
||||
|
||||
def notify(self, obj: object, message: Dict):
|
||||
for receiver in self.receivers[::-1]:
|
||||
receiver.receive_notify(obj, message)
|
||||
|
||||
def register_receiver(self, receiver: Receiver):
|
||||
self.receivers.append(receiver)
|
||||
self.notify(self, message={Signal.REGISTER: receiver})
|
||||
|
|
@ -0,0 +1,13 @@
|
|||
"""shortcut for API"""
|
||||
from idrlnet.geo_utils import *
|
||||
from idrlnet.architecture import *
|
||||
from idrlnet.pde_op import *
|
||||
from idrlnet.net import NetNode
|
||||
from idrlnet.data import get_data_node, DataNode, get_data_nodes, datanode, SampleDomain
|
||||
from idrlnet.pde import ExpressionNode
|
||||
from idrlnet.solver import Solver
|
||||
from idrlnet.callbacks import GradientReceiver
|
||||
from idrlnet.receivers import Receiver, Signal
|
||||
from idrlnet.variable import Variables, export_var
|
||||
from idrlnet.header import logger
|
||||
from idrlnet import GPU_ENABLED
|
||||
|
|
@ -0,0 +1,390 @@
|
|||
"""Solver"""
|
||||
|
||||
from collections import ChainMap
|
||||
import torch
|
||||
import os
|
||||
import pathlib
|
||||
from typing import Dict, List, Union, Tuple, Optional, Callable
|
||||
from idrlnet.callbacks import SummaryReceiver, HandleResultReceiver
|
||||
from idrlnet.header import logger
|
||||
from idrlnet.optim import Optimizable
|
||||
from idrlnet.data import DataNode, SampleDomain
|
||||
from idrlnet.net import NetNode
|
||||
from idrlnet.receivers import Receiver, Notifier, Signal
|
||||
from idrlnet.variable import Variables, DomainVariables
|
||||
from idrlnet.graph import VertexTaskPipeline
|
||||
import idrlnet
|
||||
|
||||
__all__ = ['Solver']
|
||||
|
||||
|
||||
class Solver(Notifier, Optimizable):
|
||||
"""Instances of the Solver class integrate configurations and handle the computation
|
||||
operation during solving PINNs. One problem usually needs one instance to solve.
|
||||
|
||||
:param sample_domains: A tuple of geometry domains used to sample points for training of PINNs.
|
||||
:type sample_domains: Tuple[DataNode, ...]
|
||||
:param netnodes: A list of neural networks. Trainable computation nodes.
|
||||
:type netnodes: List[NetNode]
|
||||
:param pdes: A list of partial differential equations. Similar to net nodes, they can evaluateinputs and output
|
||||
results. But they are not trainable.
|
||||
:type pdes: Optional[List[PdeNode]]
|
||||
:param network_dir: The directory used to automatically load and store ckpt files
|
||||
:type network_dir: str
|
||||
:param summary_dir: The directory is used for store information about tensorboard. If it is not specified,
|
||||
it will be assigned to network_dir by default.
|
||||
:type summary_dir: Optional[str]
|
||||
:param max_iter: Max iteration the solver would run.
|
||||
:type max_iter: int
|
||||
:param save_freq: Frequency of saving ckpt.
|
||||
:type save_freq: int
|
||||
:param print_freq: Frequency of printing loss.
|
||||
:type print_freq: int
|
||||
:param loading: By default, it is true. It will try to load ckpt and continue previous training stage.
|
||||
:type loading: bool
|
||||
:param init_network_dirs: A list of directories for loading pre-trained networks.
|
||||
:type init_network_dirs: List[str]
|
||||
:param opt_config: Configure one optimizer for all trainable parameters. It is a wrapper of `torch.optim.Optimizer`.
|
||||
One can specify any subclasses of `torch.optim.Optimizer` by
|
||||
expanding the args like:
|
||||
|
||||
- `opt_config=dict(optimizer='Adam', lr=0.001)` **by default**.
|
||||
- `opt_config=dict(optimizer='SGD', lr=0.01, momentum=0.9)`
|
||||
- `opt_config=dict(optimizer='SparseAdam', lr=0.001, betas=(0.9, 0.999), eps=1e-08)`
|
||||
Note that the opt is Case Sensitive.
|
||||
:type opt_config: Dict
|
||||
:param schedule_config: Configure one lr scheduler for the optimizer. It is a wrapper of
|
||||
|
||||
- `torch.optim.lr_scheduler._LRScheduler`. One can specify any subclasses of the class lke:
|
||||
- `schedule_config=dict(scheduler='ExponentialLR', gamma=math.pow(0.95, 0.001))`
|
||||
- `schedule_config=dict(scheduler='StepLR', step_size=30, gamma=0.1)`
|
||||
Note that the scheduler is Case Sensitive.
|
||||
:type schedule_config: Dict
|
||||
:param result_dir: save the final training domain data. defaults to 'train_domain/results'
|
||||
:type result_dir: str
|
||||
:param kwargs:
|
||||
"""
|
||||
|
||||
def __init__(self, sample_domains: Tuple[Union[DataNode, SampleDomain], ...],
|
||||
netnodes: List[NetNode],
|
||||
pdes: Optional[List] = None,
|
||||
network_dir: str = './network_dir',
|
||||
summary_dir: Optional[str] = None,
|
||||
max_iter: int = 1000,
|
||||
save_freq: int = 100,
|
||||
print_freq: int = 10,
|
||||
loading: bool = True,
|
||||
init_network_dirs: Optional[List[str]] = None,
|
||||
opt_config: Dict = None,
|
||||
schedule_config: Dict = None,
|
||||
result_dir='train_domain/results',
|
||||
**kwargs):
|
||||
|
||||
self.network_dir: str = network_dir
|
||||
self.domain_losses = {domain.name: domain.loss_fn for domain in sample_domains}
|
||||
self.netnodes: List[NetNode] = netnodes
|
||||
if init_network_dirs:
|
||||
self.init_network_dirs = init_network_dirs
|
||||
else:
|
||||
self.init_network_dirs = []
|
||||
self.init_load()
|
||||
|
||||
self.pdes: List = [] if pdes is None else pdes
|
||||
pathlib.Path(self.network_dir).mkdir(parents=True, exist_ok=True)
|
||||
self.global_step = 0
|
||||
self.max_iter = max_iter
|
||||
self.save_freq = save_freq
|
||||
self.print_freq = print_freq
|
||||
try:
|
||||
self.parse_configure(**{**({"opt_config": opt_config} if opt_config is not None else {}),
|
||||
**({"schedule_config": schedule_config} if schedule_config is not None else {})})
|
||||
except Exception:
|
||||
logger.error("Optimizer configuration failed")
|
||||
raise
|
||||
|
||||
if loading:
|
||||
try:
|
||||
self.load()
|
||||
except:
|
||||
pass
|
||||
self.sample_domains: Tuple[DataNode, ...] = sample_domains
|
||||
self.summary_dir = self.network_dir if summary_dir is None else summary_dir
|
||||
self.receivers: List[Receiver] = [SummaryReceiver(self.summary_dir), HandleResultReceiver(result_dir)]
|
||||
|
||||
@property
|
||||
def network_dir(self):
|
||||
return self._network_dir
|
||||
|
||||
@network_dir.setter
|
||||
def network_dir(self, network_dir):
|
||||
self._network_dir = network_dir
|
||||
|
||||
@property
|
||||
def sample_domains(self):
|
||||
return self._sample_domains
|
||||
|
||||
@sample_domains.setter
|
||||
def sample_domains(self, sample_domains):
|
||||
self._sample_domains = sample_domains
|
||||
self._generate_dict_index()
|
||||
self.generate_computation_pipeline()
|
||||
|
||||
@property
|
||||
def trainable_parameters(self) -> List[torch.nn.parameter.Parameter]:
|
||||
"""Return trainable parameters in netnodes. Parameters in netnodes with ``is_reference=True``
|
||||
or ``fixed=True`` will not be returned.
|
||||
:return: A list of trainable parameters.
|
||||
:rtype: List[torch.nn.parameter.Parameter]
|
||||
"""
|
||||
parameter_list = list(map(lambda _net_node: {'params': _net_node.net.parameters()},
|
||||
filter(lambda _net_node: not _net_node.is_reference and (not _net_node.fixed),
|
||||
self.netnodes)))
|
||||
if len(parameter_list) == 0:
|
||||
'''To make sure successful initialization of optimizers.'''
|
||||
parameter_list = [torch.nn.parameter.Parameter(data=torch.Tensor([0.]), requires_grad=True)]
|
||||
logger.warning("No trainable parameters found!")
|
||||
return parameter_list
|
||||
|
||||
@property
|
||||
def summary_receiver(self) -> SummaryReceiver:
|
||||
try:
|
||||
summary_receiver = self.receivers[0]
|
||||
assert isinstance(summary_receiver, SummaryReceiver)
|
||||
except IndexError:
|
||||
raise
|
||||
return summary_receiver
|
||||
|
||||
def __str__(self):
|
||||
"""return sovler information, it will return components recursively"""
|
||||
str_list = []
|
||||
str_list.append("nets: \n")
|
||||
str_list.append(''.join([str(net) for net in self.netnodes]))
|
||||
str_list.append("domains: \n")
|
||||
str_list.append(''.join([str(domain) for domain in self.sample_domains]))
|
||||
str_list.append('\n')
|
||||
str_list.append('optimizer config:\n')
|
||||
for i, _class in enumerate(type(self).mro()):
|
||||
if _class == Optimizable:
|
||||
str_list.append(super(type(self).mro()[i - 1], self).__str__())
|
||||
return ''.join(str_list)
|
||||
|
||||
def set_param_ranges(self, param_ranges: Dict):
|
||||
for domain in self.sample_domains:
|
||||
domain.sample_fn.param_ranges = param_ranges
|
||||
|
||||
def set_domain_parameter(self, domain_name: str, parameter_dict: dict):
|
||||
domain = self.get_sample_domain(domain_name)
|
||||
for key, value in parameter_dict.items():
|
||||
domain.sample_fn.__dict__[key] = value
|
||||
|
||||
def get_domain_parameter(self, domain_name: str, parameter: str):
|
||||
return self.get_sample_domain(domain_name).sample_fn.__dict__[parameter]
|
||||
|
||||
def get_sample_domain(self, name: str) -> DataNode:
|
||||
for value in self.sample_domains:
|
||||
if value.name == name:
|
||||
return value
|
||||
raise KeyError(f'domain {name} not exist!')
|
||||
|
||||
def generate_computation_pipeline(self):
|
||||
"""Generate computation pipeline for all domains.
|
||||
The change of `self.sample_domains` will triger this method.
|
||||
"""
|
||||
samples = self.sample_variables_from_domains()
|
||||
in_var, true_out, lambda_out = self.generate_in_out_dict(samples)
|
||||
self.vertex_pipelines = {}
|
||||
for domain_name, var in in_var.items():
|
||||
logger.info(f"Constructing computation graph for domain <{domain_name}>")
|
||||
self.vertex_pipelines[domain_name] = VertexTaskPipeline(self.netnodes + self.pdes, var,
|
||||
self.outvar_dict_index[domain_name])
|
||||
self.vertex_pipelines[domain_name].display(
|
||||
os.path.join(self.network_dir, f'{domain_name}_{self.global_step}.png'))
|
||||
|
||||
def forward_through_all_graph(self, invar_dict: DomainVariables,
|
||||
req_outvar_dict_index: Dict[str, List[str]]) -> DomainVariables:
|
||||
outvar_dict = {}
|
||||
for (key, req_outvar_names) in req_outvar_dict_index.items():
|
||||
outvar_dict[key] = self.vertex_pipelines[key].forward_pipeline(invar_dict[key], req_outvar_names)
|
||||
return outvar_dict
|
||||
|
||||
def append_sample_domain(self, datanode):
|
||||
self.sample_domains = self.sample_domains + (datanode,)
|
||||
|
||||
def _generate_dict_index(self) -> None:
|
||||
self.invar_dict_index = {domain.name: domain.inputs for domain in self.sample_domains}
|
||||
self.outvar_dict_index = {domain.name: domain.outputs for domain in self.sample_domains}
|
||||
self.lambda_dict_index = {domain.name: domain.lambda_outputs for domain in self.sample_domains}
|
||||
|
||||
def generate_in_out_dict(self, samples: DomainVariables) -> \
|
||||
Tuple[DomainVariables, DomainVariables, DomainVariables]:
|
||||
invar_dict = {}
|
||||
for domain, variable in samples.items():
|
||||
inner = {}
|
||||
for key, val in variable.items():
|
||||
if key in self.invar_dict_index[domain]:
|
||||
inner[key] = val
|
||||
invar_dict[domain] = inner
|
||||
|
||||
invar_dict = {
|
||||
domain: Variables({key: val for key, val in variable.items() if key in self.invar_dict_index[domain]}) for
|
||||
domain, variable in samples.items()}
|
||||
outvar_dict = {
|
||||
domain: Variables({key: val for key, val in variable.items() if key in self.outvar_dict_index[domain]}) for
|
||||
domain, variable in samples.items()}
|
||||
lambda_dict = {
|
||||
domain: Variables({key: val for key, val in variable.items() if key in self.lambda_dict_index[domain]}) for
|
||||
domain, variable in samples.items()}
|
||||
return invar_dict, outvar_dict, lambda_dict
|
||||
|
||||
def solve(self):
|
||||
"""After the solver instance is initialized, the method could be called to solve the entire problem.
|
||||
"""
|
||||
self.notify(self, message={Signal.SOLVE_START: 'default'})
|
||||
while self.global_step < self.max_iter:
|
||||
loss = self.train_pipe()
|
||||
if self.global_step % self.print_freq == 0:
|
||||
logger.info("Iteration: {}, Loss: {}".format(self.global_step, loss))
|
||||
if self.global_step % self.save_freq == 0:
|
||||
self.save()
|
||||
logger.info("Training Stage Ends")
|
||||
self.notify(self, message={Signal.SOLVE_END: 'default'})
|
||||
|
||||
def train_pipe(self):
|
||||
"""Sample once; calculate the loss once; backward propagation once
|
||||
:return: None
|
||||
"""
|
||||
self.notify(self, message={Signal.TRAIN_PIPE_START: 'defaults'})
|
||||
for opt in self.optimizers:
|
||||
opt.zero_grad()
|
||||
samples = self.sample_variables_from_domains()
|
||||
in_var, true_out, lambda_out = self.generate_in_out_dict(samples)
|
||||
pred_out_sample = self.forward_through_all_graph(in_var, self.outvar_dict_index)
|
||||
try:
|
||||
loss = self.compute_loss(in_var, pred_out_sample, true_out, lambda_out)
|
||||
except RuntimeError:
|
||||
raise
|
||||
self.notify(self, message={Signal.BEFORE_BACKWARD: 'defaults'})
|
||||
loss.backward()
|
||||
for opt in self.optimizers:
|
||||
opt.step()
|
||||
self.global_step += 1
|
||||
|
||||
for scheduler in self.schedulers:
|
||||
scheduler.step(self.global_step)
|
||||
self.notify(self, message={Signal.TRAIN_PIPE_END: 'defaults'})
|
||||
return loss
|
||||
|
||||
def compute_loss(self, in_var: DomainVariables, pred_out_sample: DomainVariables,
|
||||
true_out: DomainVariables,
|
||||
lambda_out: DomainVariables) -> torch.Tensor:
|
||||
"""Compute the total loss in one epoch.
|
||||
|
||||
"""
|
||||
diff = dict()
|
||||
for domain_name, domain_val in true_out.items():
|
||||
if len(domain_val) == 0:
|
||||
continue
|
||||
diff[domain_name] = pred_out_sample[domain_name] - domain_val.to_torch_tensor_()
|
||||
diff[domain_name].update(lambda_out[domain_name])
|
||||
diff[domain_name].update(area=in_var[domain_name]['area'])
|
||||
|
||||
for domain, var in diff.items():
|
||||
lambda_diff = dict()
|
||||
for constraint, _ in var.items():
|
||||
if 'lambda_' + constraint in in_var[domain].keys():
|
||||
lambda_diff['lambda_' + constraint] = in_var[domain]['lambda_' + constraint]
|
||||
var.update(lambda_diff)
|
||||
|
||||
self.loss_component = Variables(
|
||||
ChainMap(
|
||||
*[diff[domain_name].weighted_loss(f"{domain_name}_loss",
|
||||
loss_function=self.domain_losses[domain_name]) for
|
||||
domain_name, domain_val in
|
||||
diff.items()]))
|
||||
self.notify(self, message={Signal.BEFORE_COMPUTE_LOSS: {**self.loss_component}})
|
||||
loss = sum({domain_name: self.get_sample_domain(domain_name).sigma * self.loss_component[f"{domain_name}_loss"] for
|
||||
domain_name in diff}.values())
|
||||
self.notify(self, message={Signal.AFTER_COMPUTE_LOSS: {**self.loss_component, **{'total_loss': loss}}})
|
||||
return loss
|
||||
|
||||
def infer_step(self, domain_attr: Dict[str, List[str]]) -> DomainVariables:
|
||||
"""Specify a domain and required fields for inference.
|
||||
:param domain_attr: A map from a domain name to the list of required outputs on the domain.
|
||||
:type domain_attr: Dict[str, List[str]]
|
||||
:return: A dict of variables which are required.
|
||||
:rtype: Dict[str, Variables]
|
||||
"""
|
||||
samples = self.sample_variables_from_domains()
|
||||
in_var, true_out, lambda_out = self.generate_in_out_dict(samples)
|
||||
pred_out_sample = self.forward_through_all_graph(in_var, domain_attr)
|
||||
return pred_out_sample
|
||||
|
||||
def sample_variables_from_domains(self) -> DomainVariables:
|
||||
return {data_node.name: data_node.sample() for data_node in self.sample_domains}
|
||||
|
||||
def save(self):
|
||||
"""Save parameters of netnodes and the global step to `model.ckpt`.
|
||||
"""
|
||||
save_path = os.path.join(self.network_dir, 'model.ckpt')
|
||||
logger.info("save to path: {}".format(os.path.abspath(save_path)))
|
||||
save_dict = {f"{net_node.name}_dict": net_node.state_dict() for net_node in
|
||||
filter(lambda _net: not _net.is_reference, self.netnodes)}
|
||||
for i, opt in enumerate(self.optimizers):
|
||||
save_dict['optimizer_{}_dict'.format(i)] = opt.state_dict()
|
||||
save_dict['global_step'] = self.global_step
|
||||
torch.save(save_dict, save_path)
|
||||
|
||||
def init_load(self):
|
||||
for network_dir in self.init_network_dirs:
|
||||
save_path = os.path.join(network_dir, 'model.ckpt')
|
||||
save_dict = torch.load(save_path)
|
||||
for net_node in self.netnodes:
|
||||
if f"{net_node.name}_dict" in save_dict.keys() and not net_node.is_reference:
|
||||
net_node.load_state_dict(save_dict[f"{net_node.name}_dict"])
|
||||
logger.info(f"Successfully loading initialization {net_node.name}.")
|
||||
|
||||
def load(self):
|
||||
"""Load parameters of netnodes and the global step from `model.ckpt`.
|
||||
"""
|
||||
save_path = os.path.join(self.network_dir, 'model.ckpt')
|
||||
if not idrlnet.GPU_ENABLED:
|
||||
save_dict = torch.load(save_path, map_location=torch.device('cpu'))
|
||||
else:
|
||||
save_dict = torch.load(save_path)
|
||||
# todo: save on CPU, load on GPU
|
||||
for i, opt in enumerate(self.optimizers):
|
||||
opt.load_state_dict(save_dict['optimizer_{}_dict'.format(i)])
|
||||
self.global_step = save_dict['global_step']
|
||||
for net_node in self.netnodes:
|
||||
if f"{net_node.name}_dict" in save_dict.keys() and not net_node.is_reference:
|
||||
net_node.load_state_dict(save_dict[f"{net_node.name}_dict"])
|
||||
logger.info(f"Successfully loading {net_node.name}.")
|
||||
|
||||
def configure_optimizers(self):
|
||||
"""
|
||||
Call interfaces of ``Optimizable``
|
||||
"""
|
||||
opt = self.optimizer_config['optimizer']
|
||||
if isinstance(opt, str) and opt in Optimizable.OPTIMIZER_MAP:
|
||||
opt = Optimizable.OPTIMIZER_MAP[opt](self.trainable_parameters,
|
||||
**{k: v for k, v in self.optimizer_config.items() if k != 'optimizer'})
|
||||
elif isinstance(opt, Callable):
|
||||
opt = opt
|
||||
else:
|
||||
raise NotImplementedError(
|
||||
'The optimizer is not implemented. You may use one of the following optimizer:\n' + '\n'.join(
|
||||
Optimizable.OPTIMIZER_MAP.keys()) + '\n Example: opt_config=dict(optimizer="Adam", lr=1e-3)')
|
||||
|
||||
lr_scheduler = self.schedule_config['scheduler']
|
||||
if isinstance(lr_scheduler, str) and lr_scheduler in Optimizable.SCHEDULE_MAP:
|
||||
lr_scheduler = Optimizable.SCHEDULE_MAP[lr_scheduler](opt,
|
||||
**{k: v for k, v in self.schedule_config.items() if
|
||||
k != 'scheduler'})
|
||||
elif isinstance(lr_scheduler, Callable):
|
||||
lr_scheduler = lr_scheduler
|
||||
else:
|
||||
raise NotImplementedError(
|
||||
'The scheduler is not implemented. You may use one of the following scheduler:\n' + '\n'.join(
|
||||
Optimizable.SCHEDULE_MAP.keys()) + '\n Example: schedule_config=dict(scheduler="ExponentialLR", gamma=0.999')
|
||||
self.optimizers = [opt]
|
||||
self.schedulers = [lr_scheduler]
|
||||
|
|
@ -0,0 +1,102 @@
|
|||
"""
|
||||
conversion utils for sympy expression and torch functions.
|
||||
todo: replace sampling method in GEOMETRY
|
||||
"""
|
||||
|
||||
from sympy import lambdify, Symbol, Derivative, Function, Basic
|
||||
from sympy.utilities.lambdify import implemented_function
|
||||
from sympy.printing.str import StrPrinter
|
||||
import torch
|
||||
from idrlnet.header import DIFF_SYMBOL
|
||||
from functools import reduce
|
||||
|
||||
__all__ = ['integral', 'torch_lambdify']
|
||||
|
||||
|
||||
def integral_fun(x):
|
||||
if isinstance(x, torch.Tensor):
|
||||
return torch.sum(input=x, dim=0, keepdim=True) * torch.ones_like(x)
|
||||
return x
|
||||
|
||||
|
||||
integral = implemented_function('integral', lambda x: integral_fun(x))
|
||||
|
||||
|
||||
def torch_lambdify(r, f, *args, **kwargs):
|
||||
try:
|
||||
f = float(f)
|
||||
except:
|
||||
pass
|
||||
if isinstance(f, (float, int, bool)): # constant function
|
||||
|
||||
def loop_lambda(constant):
|
||||
return lambda **x: torch.zeros_like(next(iter(x.items()))[1]) + constant
|
||||
|
||||
lambdify_f = loop_lambda(f)
|
||||
else:
|
||||
lambdify_f = lambdify([k for k in r], f, [TORCH_SYMPY_PRINTER], *args, **kwargs)
|
||||
# lambdify_f = lambdify([k for k in r], f, *args, **kwargs)
|
||||
return lambdify_f
|
||||
|
||||
|
||||
# todo: more functions
|
||||
TORCH_SYMPY_PRINTER = {
|
||||
'sin': torch.sin,
|
||||
'cos': torch.cos,
|
||||
'tan': torch.tan,
|
||||
'exp': torch.exp,
|
||||
'sqrt': torch.sqrt,
|
||||
'Abs': torch.abs,
|
||||
'tanh': torch.tanh,
|
||||
'DiracDelta': torch.zeros_like,
|
||||
'Heaviside': lambda x: torch.heaviside(x, torch.tensor([0.])),
|
||||
'amin': lambda x: reduce(lambda y, z: torch.minimum(y, z), x),
|
||||
'amax': lambda x: reduce(lambda y, z: torch.maximum(y, z), x),
|
||||
'Min': lambda *x: reduce(lambda y, z: torch.minimum(y, z), x),
|
||||
'Max': lambda *x: reduce(lambda y, z: torch.maximum(y, z), x),
|
||||
'equal': lambda x, y: torch.isclose(x, y),
|
||||
'Xor': torch.logical_xor,
|
||||
'log': torch.log,
|
||||
'sinh': torch.sinh,
|
||||
'cosh': torch.cosh,
|
||||
'asin': torch.arcsin,
|
||||
'acos': torch.arccos,
|
||||
'atan': torch.arctan,
|
||||
}
|
||||
|
||||
|
||||
def _reduce_sum(x: torch.Tensor):
|
||||
return torch.sum(x, dim=0, keepdim=True)
|
||||
|
||||
|
||||
def _replace_derivatives(expr):
|
||||
while len(expr.atoms(Derivative)) > 0:
|
||||
deriv = expr.atoms(Derivative).pop()
|
||||
expr = expr.subs(deriv, Function(str(deriv))(*deriv.free_symbols))
|
||||
while True:
|
||||
try:
|
||||
custom_fun = {_fun for _fun in expr.atoms(Function) if
|
||||
(_fun.class_key()[1] == 0) and (not _fun.class_key()[2] == 'integral')
|
||||
}.pop()
|
||||
new_symbol_name = str(custom_fun)
|
||||
expr = expr.subs(custom_fun, Symbol(new_symbol_name))
|
||||
except KeyError:
|
||||
break
|
||||
return expr
|
||||
|
||||
|
||||
class UnderlineDerivativePrinter(StrPrinter):
|
||||
def _print_Function(self, expr):
|
||||
return expr.func.__name__
|
||||
|
||||
def _print_Derivative(self, expr):
|
||||
return "".join([str(expr.args[0].func)] + [order * (DIFF_SYMBOL + str(key)) for key, order in expr.args[1:]])
|
||||
|
||||
|
||||
def sstr(expr, **settings):
|
||||
p = UnderlineDerivativePrinter(settings)
|
||||
s = p.doprint(expr)
|
||||
return s
|
||||
|
||||
|
||||
Basic.__str__ = lambda self: sstr(self, order=None)
|
||||
|
|
@ -0,0 +1,235 @@
|
|||
"""Define variables, intermediate data format for the package."""
|
||||
|
||||
import torch
|
||||
import itertools
|
||||
from typing import List, Dict
|
||||
import numpy as np
|
||||
import os
|
||||
from pyevtk.hl import pointsToVTK
|
||||
import pathlib
|
||||
import enum
|
||||
from typing import Union
|
||||
from collections import defaultdict
|
||||
import pandas as pd
|
||||
from idrlnet.header import DIFF_SYMBOL
|
||||
|
||||
__all__ = ['Loss', 'Variables', 'DomainVariables', 'export_var']
|
||||
|
||||
|
||||
class Loss(enum.Enum):
|
||||
"""Enumerate loss functions"""
|
||||
|
||||
L1 = 'L1'
|
||||
square = 'square'
|
||||
|
||||
|
||||
class LossFunction:
|
||||
"""Manage loss functions"""
|
||||
|
||||
@staticmethod
|
||||
def weighted_loss(variables, loss_function, name):
|
||||
if loss_function == Loss.L1.name or loss_function == Loss.L1:
|
||||
return LossFunction.weighted_L1_loss(variables, name=name)
|
||||
elif loss_function == Loss.square.name or loss_function == Loss.square:
|
||||
return LossFunction.weighted_square_loss(variables, name=name)
|
||||
raise NotImplementedError(f"loss function {loss_function} is not defined!")
|
||||
|
||||
@staticmethod
|
||||
def weighted_L1_loss(variables: 'Variables', name: str) -> 'Variables':
|
||||
loss = 0.
|
||||
for key, val in variables.items():
|
||||
if key.startswith("lambda_") or key == 'area':
|
||||
continue
|
||||
elif "lambda_" + key in variables.keys():
|
||||
loss += torch.sum((torch.abs(val)) * variables["lambda_" + key] * variables["area"])
|
||||
else:
|
||||
loss += torch.sum((torch.abs(val)) * variables["area"])
|
||||
return Variables({name: loss})
|
||||
|
||||
@staticmethod
|
||||
def weighted_square_loss(variables: 'Variables', name: str) -> 'Variables':
|
||||
loss = 0.
|
||||
for key, val in variables.items():
|
||||
if key.startswith("lambda_") or key == 'area':
|
||||
continue
|
||||
elif "lambda_" + key in variables.keys():
|
||||
loss += torch.sum((val ** 2) * variables["lambda_" + key] * variables["area"])
|
||||
else:
|
||||
loss += torch.sum((val ** 2) * variables["area"])
|
||||
return Variables({name: loss})
|
||||
|
||||
|
||||
class Variables(dict):
|
||||
def __sub__(self, other: 'Variables') -> 'Variables':
|
||||
return Variables(
|
||||
{key: (self[key] if key in self else 0) - (other[key] if key in other else 0) for key in {**self, **other}})
|
||||
|
||||
def weighted_loss(self, name: str, loss_function: Union[Loss, str]) -> 'Variables':
|
||||
"""Regard the variable as residuals and reduce to a weighted_loss."""
|
||||
|
||||
return LossFunction.weighted_loss(variables=self, loss_function=loss_function, name=name)
|
||||
|
||||
def subset(self, subset_keys: List[str]) -> 'Variables':
|
||||
"""Construct a new variable with subset references"""
|
||||
|
||||
return Variables({name: self[name] for name in subset_keys if name in self})
|
||||
|
||||
def to_torch_tensor_(self) -> 'Variables[str, torch.Tensor]':
|
||||
"""Convert the variables to torch.Tensor"""
|
||||
|
||||
for key, val in self.items():
|
||||
if not isinstance(val, torch.Tensor):
|
||||
self[key] = torch.Tensor(val)
|
||||
if (not key.startswith('lambda_')) and (not key == 'area'):
|
||||
self[key].requires_grad_()
|
||||
return self
|
||||
|
||||
def to_ndarray_(self) -> 'Variables[str, np.ndarray]':
|
||||
"""convert to a numpy based variables"""
|
||||
|
||||
for key, val in self.items():
|
||||
if isinstance(val, torch.Tensor):
|
||||
self[key] = val.detach().cpu().numpy()
|
||||
return self
|
||||
|
||||
def to_ndarray(self) -> 'Variables[str, np.ndarray]':
|
||||
"""Return a new numpy based variables"""
|
||||
|
||||
new_var = Variables()
|
||||
for key, val in self.items():
|
||||
if isinstance(val, torch.Tensor):
|
||||
new_var[key] = val.detach().cpu().numpy()
|
||||
else:
|
||||
new_var[key] = val
|
||||
return new_var
|
||||
|
||||
def to_dataframe(self) -> pd.DataFrame:
|
||||
"""merge to a pandas.DataFrame"""
|
||||
|
||||
np_var = self.to_ndarray()
|
||||
keys, values = list(zip(*[(key, value) for key, value in np_var.items()]))
|
||||
values = np.concatenate([value for value in values], axis=-1)
|
||||
df = pd.DataFrame(data=values, columns=keys)
|
||||
return df
|
||||
|
||||
def merge_tensor(self) -> torch.Tensor:
|
||||
"""merge tensors in the Variable"""
|
||||
|
||||
variable_list = [value for _, value in self.items()]
|
||||
variable_tensor = torch.cat(variable_list, dim=-1)
|
||||
return variable_tensor
|
||||
|
||||
@classmethod
|
||||
def from_tensor(cls, tensor: torch.Tensor, variable_names: List[str]):
|
||||
"""Construct Variables from torch.Tensor"""
|
||||
|
||||
split_tensor = torch.split(tensor, 1, dim=-1)
|
||||
assert len(variable_names) == len(split_tensor)
|
||||
variables = cls()
|
||||
for name, var_t in zip(variable_names, split_tensor):
|
||||
variables[name] = var_t
|
||||
return variables
|
||||
|
||||
def differentiate_one_step_(self: 'Variables', independent_var: 'Variables', required_derivatives: List[str]):
|
||||
"""One order of derivatives will be computed towards the required_derivatives."""
|
||||
|
||||
required_derivatives = [d for d in required_derivatives if d not in self]
|
||||
required_derivatives_set = set(
|
||||
tuple(required_derivative.split(DIFF_SYMBOL)) for required_derivative in required_derivatives)
|
||||
dependent_var_set = set(tuple(dv.split(DIFF_SYMBOL)) for dv in self.keys())
|
||||
computable_derivative_dict = defaultdict(set)
|
||||
for dv, rd in itertools.product(dependent_var_set, required_derivatives_set):
|
||||
if len(rd) > len(dv) and rd[:len(dv)] == dv and rd[:len(dv) + 1] not in dependent_var_set:
|
||||
computable_derivative_dict[rd[len(dv)]].add(DIFF_SYMBOL.join(dv))
|
||||
derivative_variables = Variables()
|
||||
for key, value in computable_derivative_dict.items():
|
||||
for v in value:
|
||||
f__x = torch.autograd.grad(self[v],
|
||||
independent_var[key],
|
||||
grad_outputs=torch.ones_like(self[v]),
|
||||
retain_graph=True,
|
||||
create_graph=True,
|
||||
allow_unused=True)[0]
|
||||
if f__x is not None:
|
||||
f__x.requires_grad_()
|
||||
else:
|
||||
f__x = torch.zeros_like(self[v], requires_grad=True)
|
||||
derivative_variables[DIFF_SYMBOL.join([v, key])] = f__x
|
||||
self.update(derivative_variables)
|
||||
|
||||
def differentiate_(self: 'Variables', independent_var: 'Variables', required_derivatives: List[str]):
|
||||
"""Derivatives will be computed towards the required_derivatives"""
|
||||
|
||||
n_keys = 0
|
||||
new_keys = len(self.keys())
|
||||
while new_keys != n_keys:
|
||||
n_keys = new_keys
|
||||
self.differentiate_one_step_(independent_var, required_derivatives)
|
||||
new_keys = len(self.keys())
|
||||
|
||||
@staticmethod
|
||||
def var_differentiate_one_step(dependent_var: 'Variables', independent_var: 'Variables',
|
||||
required_derivatives: List[str]):
|
||||
"""Perform one step of differentiate towards the required_derivatives"""
|
||||
|
||||
dependent_var.differentiate_one_step_(independent_var, required_derivatives)
|
||||
|
||||
def to_csv(self, filename: str) -> None:
|
||||
"""Export variable to csv"""
|
||||
|
||||
if not filename.endswith('.csv'):
|
||||
filename += '.csv'
|
||||
df = self.to_dataframe()
|
||||
df.to_csv(filename, index=False)
|
||||
|
||||
def to_vtu(self, filename: str, coordinates=None) -> None:
|
||||
"""Export variable to vtu"""
|
||||
|
||||
coordinates = ['x', 'y', 'z'] if coordinates is None else coordinates
|
||||
shape = 0
|
||||
for axis in coordinates:
|
||||
if axis not in self.keys():
|
||||
self[axis] = np.zeros_like(next(iter(self.values())))
|
||||
else:
|
||||
shape = (len(self[axis]), 1)
|
||||
for key, value in self.items():
|
||||
if value.shape == (1, 1):
|
||||
self[key] = np.ones(shape) * value
|
||||
self[key] = np.asarray(self[key], dtype=np.float64)
|
||||
pointsToVTK(filename,
|
||||
self[coordinates[0]][:, 0].copy(),
|
||||
self[coordinates[1]][:, 0].copy(),
|
||||
self[coordinates[2]][:, 0].copy(),
|
||||
data={key: value[:, 0].copy() for key, value in self.items()})
|
||||
|
||||
def save(self, path, formats=None):
|
||||
"""Export variable to various formats"""
|
||||
|
||||
if formats is None:
|
||||
formats = ['np', 'csv', 'vtu']
|
||||
np_var = self.to_ndarray()
|
||||
if 'np' in formats:
|
||||
np.savez(path, **np_var)
|
||||
if 'csv' in formats:
|
||||
np_var.to_csv(path)
|
||||
if 'vtu' in formats:
|
||||
np_var.to_vtu(filename=path)
|
||||
|
||||
@staticmethod
|
||||
def cat(*var_list) -> 'Variables':
|
||||
"""todo: catenate in var list"""
|
||||
return Variables()
|
||||
|
||||
|
||||
DomainVariables = Dict[str, Variables]
|
||||
|
||||
|
||||
def export_var(domain_var: DomainVariables, path='./inference_domain/results', formats=None):
|
||||
"""Export a dict of variables to ``csv``, ``vtu`` or ``npz``."""
|
||||
|
||||
if formats is None:
|
||||
formats = ['csv', 'vtu', 'np']
|
||||
path = pathlib.Path(path)
|
||||
path.mkdir(exist_ok=True, parents=True)
|
||||
for key in domain_var.keys():
|
||||
domain_var[key].save(os.path.join(path, f'{key}'), formats)
|
||||
|
|
@ -0,0 +1,21 @@
|
|||
transforms3d
|
||||
typing
|
||||
numpy
|
||||
keras
|
||||
h5py
|
||||
pandas
|
||||
zipfile36
|
||||
scikit-optimize
|
||||
pytest
|
||||
sphinx
|
||||
matplotlib
|
||||
myst_parser
|
||||
sphinx_markdown_parser
|
||||
sphinx_rtd_theme==0.5.2
|
||||
tensorboard==2.4.1
|
||||
sympy==1.5.1
|
||||
pyevtk==1.1.1
|
||||
flask==1.1.2
|
||||
requests==2.25.0
|
||||
torch==1.7.1
|
||||
networkx==2.5.1
|
||||
|
|
@ -0,0 +1,22 @@
|
|||
import setuptools
|
||||
|
||||
with open("README.md", "r") as fh:
|
||||
long_description = fh.read()
|
||||
|
||||
setuptools.setup(
|
||||
name="idrlnet", # Replace with your own username
|
||||
version="0.0.1",
|
||||
author="Intelligent Design & Robust Learning lab",
|
||||
author_email="weipeng@deepinfar.cn",
|
||||
description="IDRLnet",
|
||||
long_description=long_description,
|
||||
long_description_content_type="text/markdown",
|
||||
url="https://github.com/idrl-lab/idrlnet",
|
||||
packages=setuptools.find_packages(),
|
||||
classifiers=[
|
||||
"Programming Language :: Python :: 3",
|
||||
"License :: OSI Approved :: MIT License",
|
||||
"Operating System :: OS Independent",
|
||||
],
|
||||
python_requires='>=3.6',
|
||||
)
|
||||
Loading…
Reference in New Issue