idrlnet/docs/user/get_started/8_volterra_ide.md

Volterra Integral Differential Equation

We consider the first-order Volterra type integro-differential equation on [0, 5] (from Lu et al. 2021):

\frac{d y}{d x}+y(x)=\int_{0}^{x} e^{t-x} y(t) d t, \quad y(0)=1

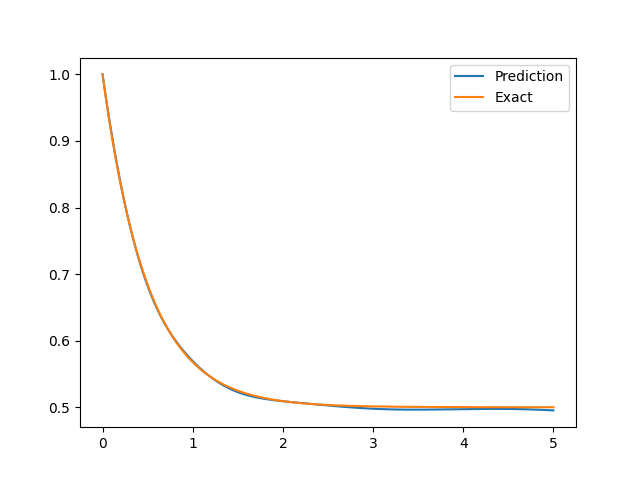
with the ground truth u=\exp(-x) \cosh x.

1D integral with Variable Limits

The LHS is represented by

exp_lhs = sc.ExpressionNode(expression=f.diff(x) + f, name='lhs')

The RHS has an integral with variable limits. Therefore, we introduce the class Int1DNode:

fs = sp.Symbol('fs')
exp_rhs = sc.Int1DNode(expression=sp.exp(s - x) * fs, var=s, lb=0, ub=x, expression_name='rhs',
                       funs={'fs': {'eval': netnode,
                                    'input_map': {'x': 's'},
                                    'output_map': {'f': 'fs'}}},
                       degree=10)

We map f and x to fs and s in the integral, respectively. The numerical integration is approximated by Gauss–Legendre quadrature with degree=10. The difference between the RHS and the LHS is presented by a pde_op.opterator.Difference node,

diff = sc.Difference(T='lhs', S='rhs', dim=1, time=False)

which generates a node with

• input=(lhs,rhs);
• output=(difference_lhs_rhs,).

The final result is shown as follows:

See examples/Volterra_IDE.