idrlnet/docs/user/get_started/2_euler_beam.md

Euler–Bernoulli beam

We consider the Euler–Bernoulli beam equation,

\begin{align}
\frac{\partial^{2}}{\partial x^{2}}\left(\frac{\partial^{2} u}{\partial x^{2}}\right)=-1 \\
u|_{x=0}=0, u^{\prime}|_{x=0}=0, \\
u^{\prime \prime}|_{x=1}=0, u^{\prime \prime \prime}|_{x=1}=0,
\end{align}

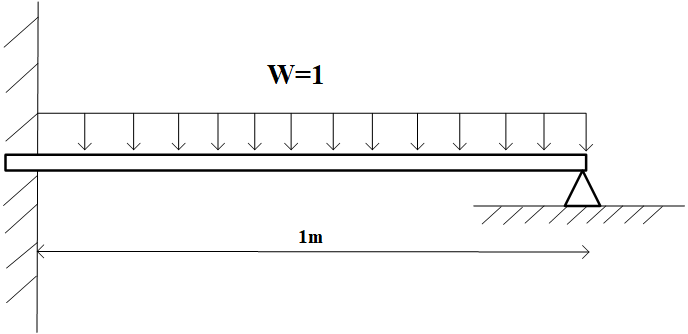
which models the following beam with external forces.

Expression Node

The Euler-Bernoulli beam equation is not implemented inside IDRLnet. Users may add the equation to idrlnet.pde_op.equations. However, one may also define the differential equation via symbol expressions directly.

First, we define a function symbol in the symbol definition part.

x = sp.symbols('x')
y = sp.Function('y')(x)

In the PDE definition part, we add these PDE nodes:

pde1 = sc.ExpressionNode(name='dddd_y', expression=y.diff(x).diff(x).diff(x).diff(x) + 1)
pde2 = sc.ExpressionNode(name='d_y', expression=y.diff(x))
pde3 = sc.ExpressionNode(name='dd_y', expression=y.diff(x).diff(x))
pde4 = sc.ExpressionNode(name='ddd_y', expression=y.diff(x).diff(x).diff(x))

These are instances of idrl.pde.PdeNode, which are also computational nodes. For example, pde1 is an instance of Node with

• inputs=tuple();
• derivatives=(y__x__x__x__x, );
• outputs=('dddd_y',).

The four PDE nodes match the following operators, respectively:

• dy^4/d^4x+1;
• dy/dx;
• dy^2/d^2x;
• dy^3/d^3x.

Seperate Inference Domain

In this example, we define a domain specified for inference.

@sc.datanode(name='infer')
class Infer(sc.SampleDomain):
    def sampling(self, *args, **kwargs):
        return {'x': np.linspace(0, 1, 1000).reshape(-1, 1)}, {}

Its instance is not be passed to the solver initializer, which may improve the performance since Infer().sampling After the solving procedure ends, we change the sample_domains of the solver,

solver.sample_domains = (Infer(),)

which triggers the regeneration of the computational graph. Then solver.infer_step() is called.

points = solver.infer_step({'infer': ['x', 'y']})
xs = points['infer']['x'].detach().cpu().numpy().ravel()
y_pred = points['infer']['y'].detach().cpu().numpy().ravel()

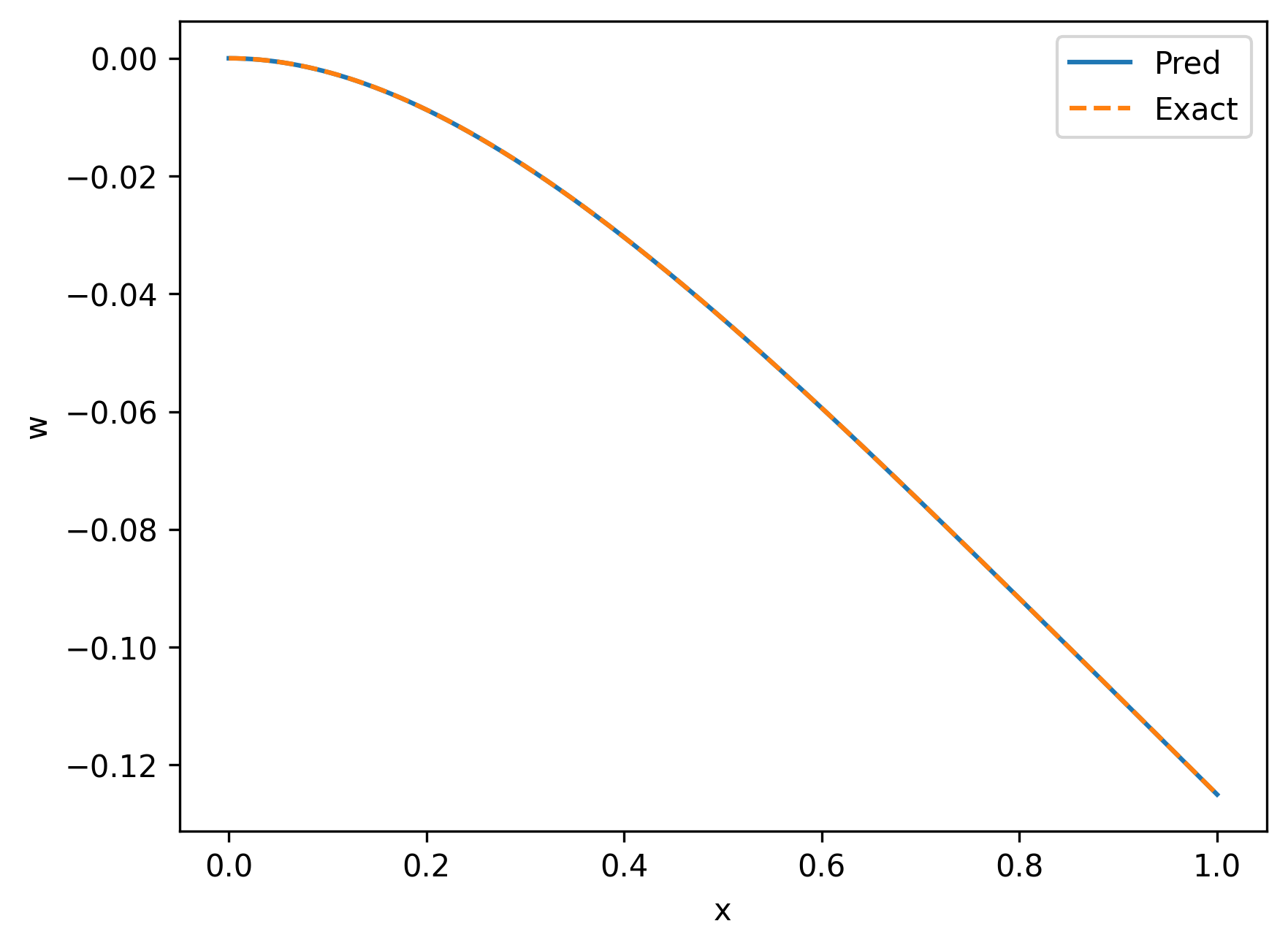
The result is shown as follows.

See examples/euler_beam.