idrlnet/docs/user/get_started/6_parameterized_poisson.md

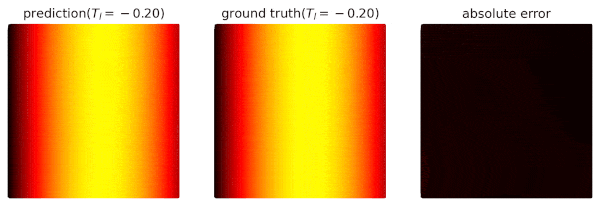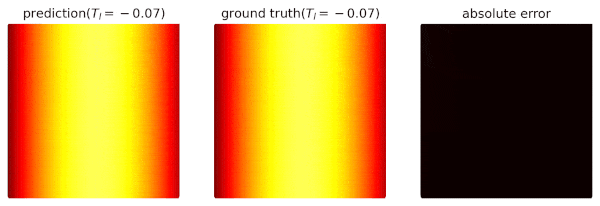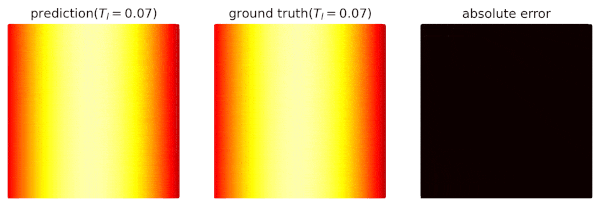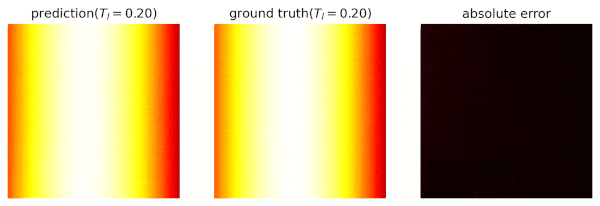
Parameterized Poisson

We consider an extended problem of Simple Poisson.

\begin{array}{l}
-\Delta u=1\\
\frac{\partial u(x, -1)}{\partial n}=\frac{\partial u(x, 1)}{\partial n}=0 \\
u(-1,y)=T_l\\
u(1, y)=0,
\end{array}

where T_l is a design parameter ranging in (-0.2,0.2). The target is to train a surrogate that u_\theta(x,y,T_l) gives the temperature at (x,y) when T_l is provided.

Train A Surrogate

In addition, we define the parameter

temp = sp.Symbol('temp')
temp_range = {temp: (-0.2, 0.2)}

The usage of temp is similar to the time variable in Burgers' Equation. temp_range should be passed to the argument param_ranges in sampling domains.

The left bound value condition is

@sc.datanode
class Left(sc.SampleDomain):
    # Due to `name` is not specified, Left will be the name of datanode automatically
    def sampling(self, *args, **kwargs):
        points = rec.sample_boundary(1000, sieve=(sp.Eq(x, -1.)), param_ranges=temp_range)
        constraints = sc.Variables({'T': temp})
        return points, constraints

The result is shown as follows:

See examples/parameterized_poisson.