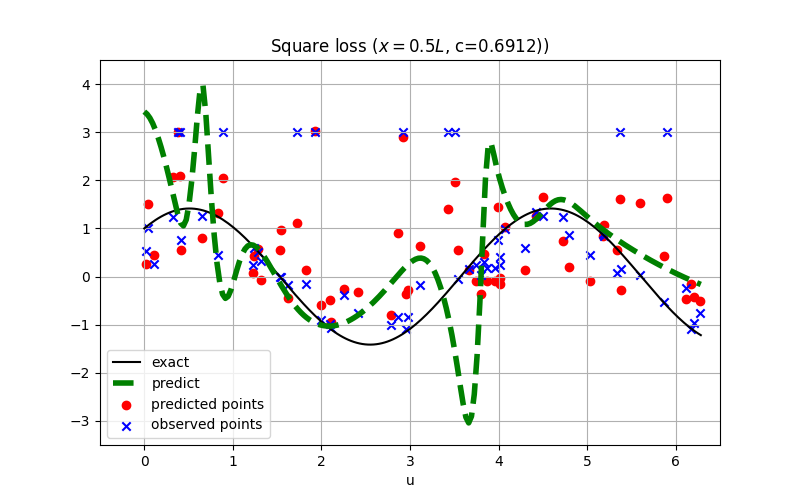
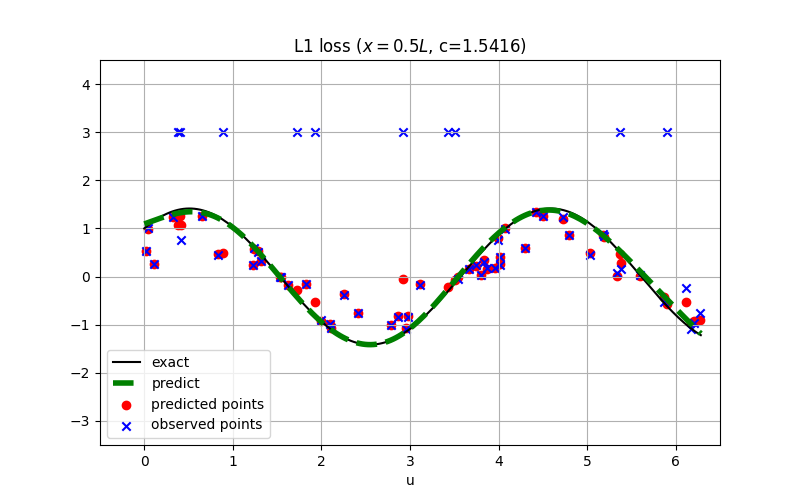
3.4 KiB
Inverse Wave Equation
Consider the 1d wave equation:
\begin{equation}
\frac{\partial^2u}{\partial t^2}=c^2\frac{\partial^2u}{\partial x^2},
\end{equation}
where c>0 is unknown and is to be estimated. A group of data pairs \{x_i, t_i, u_i\}_{i=1,2,\cdot,N} is observed.
Then the problem is formulated as:
\min_{u,c} \sum_{i=1,2,\cdots,N} \|u(x_i, t_i)-u_i\|^2\\
s.t. \frac{\partial^2u}{\partial t^2}=c^2\frac{\partial^2u}{\partial x^2}
In the context of PINN, u is parameterized to u_\theta.
The problem above is transformed to the discrete form:
\min_{\theta,c}
w_1\sum_{i=1,2,\cdots,N} \|u_\theta(x_i, t_i)-u_i\|^2
+w_2\sum_{i=1,2,\cdots,M}\left|\frac{\partial^2u_\theta(x_i,t_i)}{\partial t^2}-c^2\frac{\partial^2u_\theta(x_i,t_i)}{\partial x^2}\right|^2.
Importing External Data
We take the ground truth
u=\sin x \cdot(\sin 1.54 t + \cos 1.54 t),
where c=1.54.
The external data is generated by
points = geo.sample_interior(density=20,
bounds={x: (0, L)},
param_ranges=time_range,
low_discrepancy=True)
points['u'] = np.sin(points['x']) * (np.sin(c * points['t']) + np.cos(c * points['t']))
# Some data points are contaminated.
points['u'][np.random.choice(len(points['u']), 10, replace=False)] = 3.
To use the external data as the data source, we define a data node to store the state:
@sc.datanode(name='wave_domain', loss_fn='L1')
class WaveExternal(sc.SampleDomain):
def __init__(self):
points = pd.read_csv('external_sample.csv')
self.points = {col: points[col].to_numpy().reshape(-1, 1) for col in points.columns}
self.constraints = {'u': self.points['u']}
self.points.pop('u')
def sampling(self, *args, **kwargs):
points = self.points
constraints = self.constraints
return points, constraints
If large-scale external data are used, users can also implement the sampling() method to adapt to external data interfaces.
Define Unknown Parameters
IDRLnet defines a network node with a single parameter to represent the variable.
var_c = sc.get_net_node(inputs=('x',), outputs=('c',), arch=sc.Arch.single_var)
If bounds for variables are available, users can embed the bounds into the definition.
var_c = sc.get_net_node(inputs=('x',), outputs=('c',), arch=sc.Arch.bounded_single_var, lower_bound=1., upper_bound=3.0)
Loss Metrics
The final loss in each iteration is represented by
loss = \sum_i^M \sigma_i \sum_j^{N_{i}} \lambda_{ij}\times\text{area}_{ij}\times\text{Loss}(y_j, y^{pred}_j),
where M domains are included, and the i-th domain has N_{i} sample points in it.
- By default, The loss function is set to
square, and the alternative isL1. More types will be implemented later. \text{area}_{ij}is the weight generated by geometric objects automatically.\sigma_iis the weight for thei-th domain loss, which is set to1.by default.\lambda_{ij}is the weight for each point.
For robust regression, the L1 loss is usually preferred over the square loss.
The conclusion might also hold for inverse PINN as shown:
See examples/inverse_wave_equation.