forked from idrl/idrlnet
58 lines
1.9 KiB
Markdown
58 lines
1.9 KiB
Markdown
# Burgers' Equation
|
|
Burgers' equation is formulated as following:
|
|
|
|
$$
|
|
\begin{equation}
|
|
\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=\nu \frac{\partial^{2} u}{\partial x^{2}}
|
|
\end{equation}
|
|
$$
|
|
We have added the template of the equation into `idrlnet.pde_op.equations`.
|
|
In this example, we take $\nu=-0.01/\pi$, and the problem is
|
|
|
|
$$
|
|
\begin{equation}
|
|
\begin{array}{l}
|
|
u_t+u u_{x}-(0.01 / \pi) u_{x x}=0, \quad x \in[-1,1], \quad t \in[0,1] \\
|
|
u(0, x)=-\sin (\pi x) \\
|
|
u(t,-1)=u(t, 1)=0
|
|
\end{array}
|
|
\end{equation}.
|
|
$$
|
|
|
|
## Time-dependent Domain
|
|
The equation is time-dependent. In addition, we define a time symbol `t` and its range.
|
|
```python
|
|
t_symbol = Symbol('t')
|
|
time_range = {t_symbol: (0, 1)}
|
|
```
|
|
The parameter range `time_range` will be passed to methods `geo.Geometry.sample_interior()` and `geo.Geometry.sample_boundary()`.
|
|
The sampling methods generate samples containing the additional dims provided in `param_ranges.keys()`.
|
|
```python
|
|
# Interior domain
|
|
points = geo.sample_interior(10000, bounds={x: (-1., 1.)}, param_ranges=time_range)
|
|
|
|
# Initial value condition
|
|
points = geo.sample_interior(100, param_ranges={t_symbol: 0.0})
|
|
|
|
# Boundary condition
|
|
points = geo.sample_boundary(100, param_ranges=time_range)
|
|
```
|
|
|
|
The result is shown as follows:
|
|
|
|
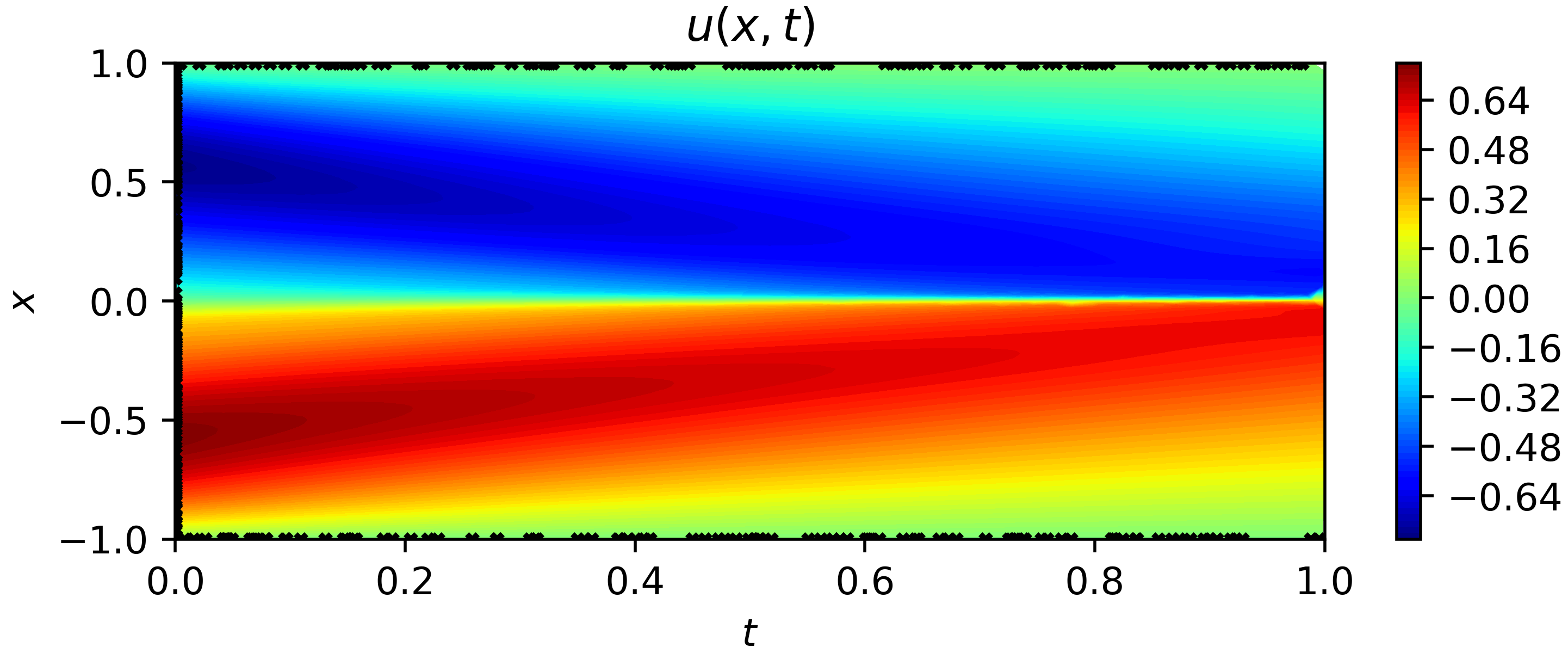
|
|
|
|
## Use TensorBoard
|
|
To monitor the training process, we employ [TensorBoard](https://www.tensorflow.org/tensorboard).
|
|
The learning rate, losses on different domains, and the total loss will be recorded automatically.
|
|
Users can call `Solver.summary_receiver()` to get the instance of `SummaryWriter`.
|
|
As default, one starts TensorBoard at `./network_idr`:
|
|
```bash
|
|
tensorboard --logdir ./network_dir
|
|
```
|
|
Users can monitor the status of training:
|
|
|
|
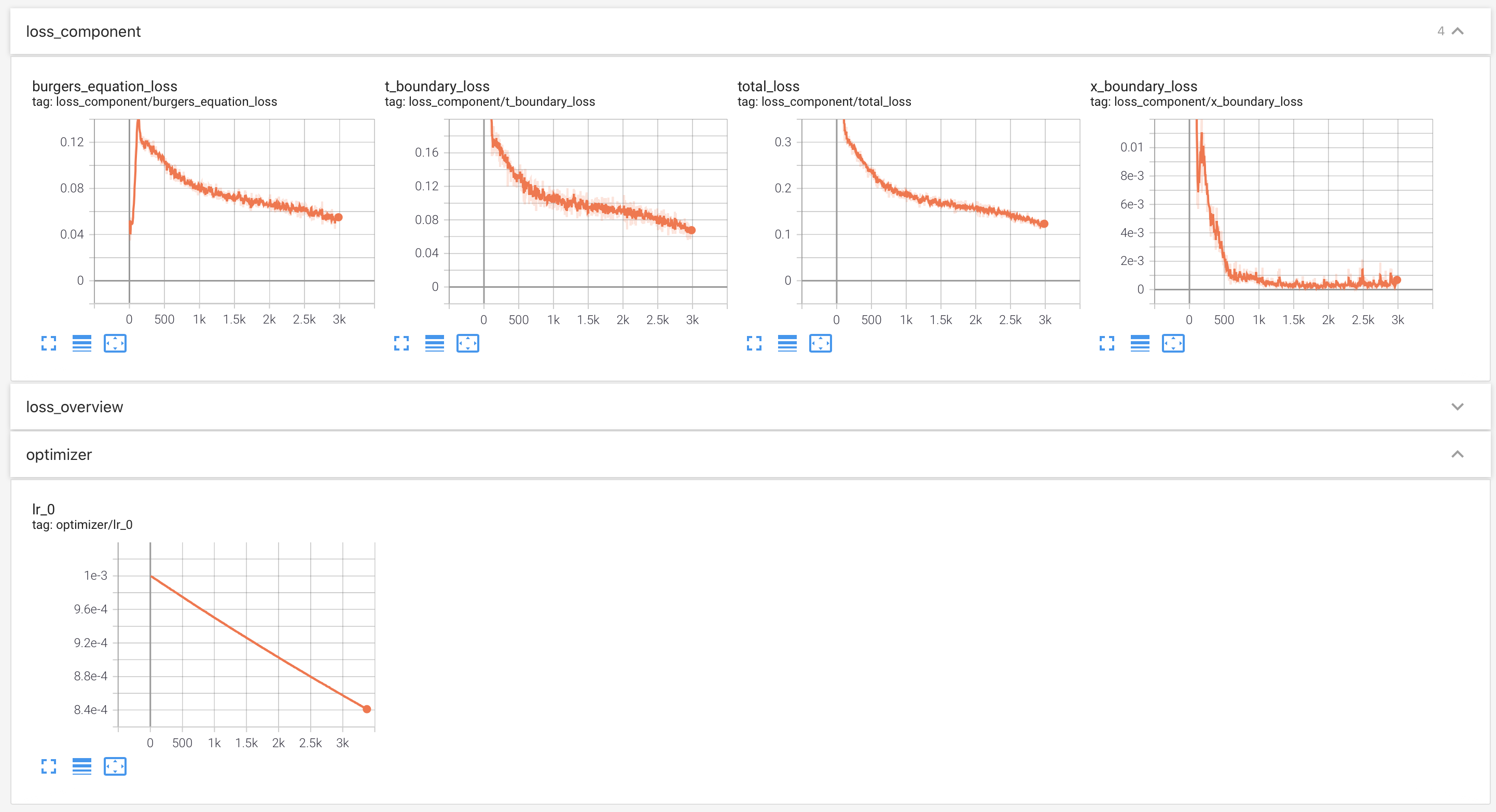
|
|
|
|
|
|
See `examples/burgers_equation`. |