forked from p94628173/idrlnet
1.4 KiB
1.4 KiB
Volterra Integral Differential Equation
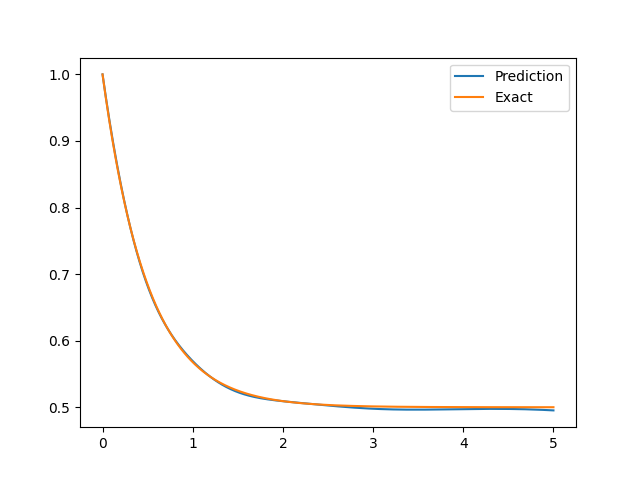
We consider the first-order Volterra type integro-differential equation on [0, 5] (from Lu et al. 2021):
\frac{d y}{d x}+y(x)=\int_{0}^{x} e^{t-x} y(t) d t, \quad y(0)=1
with the ground truth u=\exp(-x) \cosh x.
1D integral with Variable Limits
The LHS is represented by
exp_lhs = sc.ExpressionNode(expression=f.diff(x) + f, name='lhs')
The RHS has an integral with variable limits. Therefore, we introduce the class Int1DNode:
fs = sp.Symbol('fs')
exp_rhs = sc.Int1DNode(expression=sp.exp(s - x) * fs, var=s, lb=0, ub=x, expression_name='rhs',
funs={'fs': {'eval': netnode,
'input_map': {'x': 's'},
'output_map': {'f': 'fs'}}},
degree=10)
We map f and x to fs and s in the integral, respectively.
The numerical integration is approximated by Gauss–Legendre quadrature with degree=10.
The difference between the RHS and the LHS is presented by a pde_op.opterator.Difference node,
diff = sc.Difference(T='lhs', S='rhs', dim=1, time=False)
which generates a node with
input=(lhs,rhs);output=(difference_lhs_rhs,).
The final result is shown as follows:
See examples/Volterra_IDE.